题目内容
9．已知一次函数y=kx+b的图象过点（-4，0）和（0，2）．（1）画出函数的图象，求k，b的值；
（2）分别求当x=-2或x=2时的函数值．然后根据图象看一下，对吗？
分析 （1）将两点坐标代入函数表达式中，用待定系数法求解即可；用两点法画函数的图象（确定两点，描点，连线）．
（2）把x=-2或x=2代入解析式，算出对应的y的值．
解答 解：（1）由题意得：$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$，
故一次函数的解析式是：y=$\frac{1}{2}$x+2．
画出函数图象如图：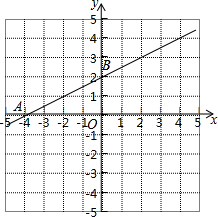
（2）当x=-2时，y=$\frac{1}{2}$x+2=1，
当x=2时，y=$\frac{1}{2}$x+2=3．
点评 本题主要考查了一次函数图象的画法以及用待定系数法求函数解析式的方法．
练习册系列答案
教材全解字词句篇系列答案
相关题目
4．
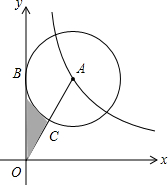如图，在平面直角坐标系xOy中，⊙A切y轴于点B，且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$（x＞0）的图象上，连接OA交⊙A于点C，且点C为OA中点，则图中阴影部分的面积为（ ）
如图，在平面直角坐标系xOy中，⊙A切y轴于点B，且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$（x＞0）的图象上，连接OA交⊙A于点C，且点C为OA中点，则图中阴影部分的面积为（ ）| A． | 4$\sqrt{3}$-$\frac{π}{3}$ | B． | 4$\sqrt{3}-\frac{2π}{3}$ | C． | 2$\sqrt{3}-\frac{π}{3}$ | D． | 2$\sqrt{3}-\frac{2π}{3}$ |