题目内容
19.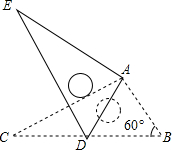 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 根据旋转的性质得AD=AB,则根据等边三角形的判定方法可判断△ABD为等边三角形,然后根据等边三角形的面积公式求解.
解答 解:∵Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD为等边三角形,
∴△ABD的面积=$\frac{\sqrt{3}}{4}$AB2=$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{4}$.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△ABD为等边三角形.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14. 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )| A. | -2a+b | B. | -b | C. | -2a-b | D. | b |
4.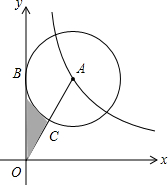 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}-\frac{2π}{3}$ | C. | 2$\sqrt{3}-\frac{π}{3}$ | D. | 2$\sqrt{3}-\frac{2π}{3}$ |
8.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.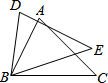 如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
 如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )
如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )| A. | AC=DE,∠C=∠E | B. | BD=AB,AC=DE | C. | AB=DB,∠A=∠D | D. | ∠C=∠E,∠A=∠D |