题目内容
8.先化简,再求值:($\frac{1}{x}$-$\frac{1}{x+1}$)•$\frac{x\sqrt{{x}^{2}+2x+1}}{(x+1)^{2}(x-1)^{2}}$,其中x是不等式组$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$的整数解.分析 先对原分式化简,再解出不等式组$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$的整数解,然后根据x是不等式组$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$的整数解,分类对原分式求值即可解答本题.
解答 解:($\frac{1}{x}$-$\frac{1}{x+1}$)•$\frac{x\sqrt{{x}^{2}+2x+1}}{(x+1)^{2}(x-1)^{2}}$
=$\frac{(x+1)-x}{x(x+1)}•\frac{x\sqrt{(x+1)^{2}}}{(x+1)^{2}(x-1)^{2}}$
=$\frac{x+1-x}{x(x+1)}•\frac{x|x+1|}{(x+1)^{2}(x-1)^{2}}$
=$\frac{|x+1|}{(x+1)^{3}(x-1)^{2}}$,
解$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$得-2≤x<1,
∵x是不等式组$\left\{\begin{array}{l}{3(x+1)>4x+2}\\{\frac{x}{2}≥\frac{x-1}{3}}\end{array}\right.$的整数解,
∴x=-2或x=-1或x=0,
当x=-2时,原式=$\frac{|-2+1|}{(-2+1)^{3}(-2-1)^{2}}=\frac{1}{-1×9}=-\frac{1}{9}$;
当x=-1时,∵x+1=0,故x=-1时,原分式无意义;
当x=0时,原分式中的$\frac{1}{x}$无意义;
故原分式的值是-$\frac{1}{9}$.
点评 本题考查分式的化简求值、解一元一次不等式的整数解,解题的关键是会对分式化简求值,会解一元一次不等式,注意代入分式的x的值必须使得原分式有意义.

| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
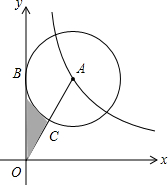 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}-\frac{2π}{3}$ | C. | 2$\sqrt{3}-\frac{π}{3}$ | D. | 2$\sqrt{3}-\frac{2π}{3}$ |