题目内容
12. 如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:
如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:(1)点P2的坐标;
(2)点P100的坐标.
分析 (1)根据旋转的旋转可直接求得P1的坐标,进而得出P2的坐标.
(2)先找到各个点所在坐标轴的位置.得到8个点将转一圈:即回到x轴.那么应让100÷8=12…4可得所求的点在x轴的负半轴上,利用OP2=21=2;OP4=22=4,则OP100=2100,进而可得点P100的坐标.
解答 解:(1)∵点P0的坐标为(1,0),
∴OP0=1,
∴OP1=1,
∵OP2=2OP1,
∴OP2=2,
∴P2的坐标为(0,2);
(2)∵OP2=21=2;OP4=22=4,
∴OP100=2100,
∵每8个点将转一圈回到x轴,
∴100÷8=12×8+4.
∴点P100在x轴负半轴上.
∴P100的坐标是(-2100,0).
点评 本题主要考查对坐标与图形变换-旋转等知识点的理解和掌握,解决本题的关键是通过作图,分析,观察,得到相应的规律.

练习册系列答案
相关题目
16.在同一坐标系中,一次函数y=x+m(m为常数)与一次函数y=-$\sqrt{3}$x+n(n为常数)图象的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
4.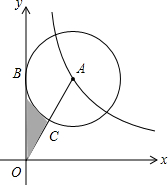 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}-\frac{2π}{3}$ | C. | 2$\sqrt{3}-\frac{π}{3}$ | D. | 2$\sqrt{3}-\frac{2π}{3}$ |
1.下列运动属于平移的是( )
| A. | 看书时候翻页 | B. | 人随着电梯在运动 | ||
| C. | 士兵听从口令向后转 | D. | 汽车到路口转弯 |