题目内容
19. 如图,△ABC是等边三角形,∠ABC和∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠A2015BC的平分线与∠A2015CD的平分线交于点A2016,则∠A2016的度数是( )
如图,△ABC是等边三角形,∠ABC和∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠A2015BC的平分线与∠A2015CD的平分线交于点A2016,则∠A2016的度数是( )| A. | $\frac{15°}{{2}^{2013}}$ | B. | $\frac{15°}{{2}^{2014}}$ | C. | $\frac{15°}{{2}^{2015}}$ | D. | $\frac{15°}{{2}^{2016}}$ |
分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,然后整理得到∠A1=$\frac{1}{2}$∠A,同理可得∠A2=$\frac{1}{2}$∠A1,从而判断出后一个角是前一个角的$\frac{1}{2}$,然后表示出,∠An即可.
解答 解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
∴∠A1+∠A1BC=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠A1BC,
∴∠A1=$\frac{1}{2}$∠A=30,
同理可得∠A2=$\frac{1}{2}$∠A1=150,
…,
∠An=$\frac{60}{{2}^{n}}$.
所以∠A2016=$\frac{15}{{2}^{2014}}$.
故选:B.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的$\frac{1}{2}$是解题的关键.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
9. 如图,直线c与直线a、b相交,且a∥b,则结论:
如图,直线c与直线a、b相交,且a∥b,则结论:
①∠1=∠2;②∠3+∠4=180°;③∠3=∠2;④∠1=∠4;⑤∠4+∠2=180°;⑥∠1=∠3;
其中正确的个数为( )
 如图,直线c与直线a、b相交,且a∥b,则结论:
如图,直线c与直线a、b相交,且a∥b,则结论:①∠1=∠2;②∠3+∠4=180°;③∠3=∠2;④∠1=∠4;⑤∠4+∠2=180°;⑥∠1=∠3;
其中正确的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.下列定理中,逆命题不成立的是( )
| A. | 两直线平行,内错角相等 | B. | 直角三角形两锐角互余 | ||
| C. | 对顶角相等 | D. | 同位角相等,两直线平行 |
4.从四边形的一个顶点出发,可得一条对角线;从五边形的一个顶点出发可得二条对角线;从六边形的一个顶点出发可得三条对角线;…按此规律,从n(n≥4,且n是整数)边形的一个顶点出发可得对角线(n-3)条.
9.在△ABC中,AB=2,BC=$\sqrt{3}$,AC=$\sqrt{7}$,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
 按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置:
按照事件发生概率的大小,将表示该事件的序号标在数轴适当位置: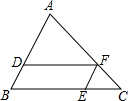 如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.
如图,在△ABC中,点D,F,E分别在边AB,AC,BC上,且DF∥BC,EF∥AB,若AD=2BD,则$\frac{CE}{BE}$的值为$\frac{1}{2}$.