题目内容
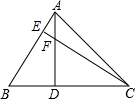 △ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )
△ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )| A、40° | B、45° |
| C、50° | D、60° |
考点:全等三角形的判定与性质
专题:
分析:由条件可以得出∠B=∠DFC,就可以得出△ADB≌△CDF就可以得出AD=CD,由等腰直角三角形的性质就可以得出结论.
解答:
解:∵AD⊥BC于D,CE⊥AB于E,
∴∠ADB=∠ADC=∠AEC=90°,
∴∠BAD+∠B=90°,∠BAD+∠AFE=90°,
∴∠B=∠AFE.
∵∠AFE=∠DFC,
∴∠B=∠DFC.
在△ADB和△CDF中,
,
∴△ADB≌△CDF(AAS),
∴AD=CD,
∴∠DAC=∠ACD.
∵∠DAC+∠ACD=90°,
∴∠ACD=45°,即∠ACB=45°.
故选B.
∴∠ADB=∠ADC=∠AEC=90°,
∴∠BAD+∠B=90°,∠BAD+∠AFE=90°,
∴∠B=∠AFE.
∵∠AFE=∠DFC,
∴∠B=∠DFC.
在△ADB和△CDF中,
|
∴△ADB≌△CDF(AAS),
∴AD=CD,
∴∠DAC=∠ACD.
∵∠DAC+∠ACD=90°,
∴∠ACD=45°,即∠ACB=45°.
故选B.
点评:本题考查了垂直的性质的运用,等腰直角三角形的判定及性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
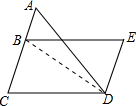 如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中,
如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中,
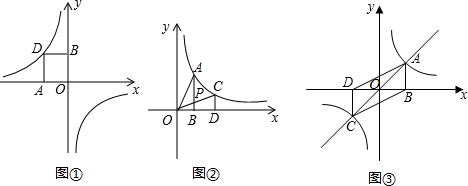
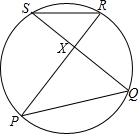 已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为
已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为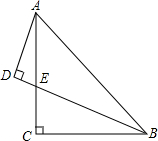 如图,在Rt△ABC中,∠C=90°,AC=BC,BE平分∠ABC交AC于E,点D在BE的延长线上,AD⊥BE.
如图,在Rt△ABC中,∠C=90°,AC=BC,BE平分∠ABC交AC于E,点D在BE的延长线上,AD⊥BE.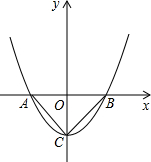 抛物线y=2x2-m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.
抛物线y=2x2-m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.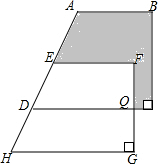 如图,两个直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移距离为AE的长度,其中HG=20cm,QC=5cm,QG=8cm,求阴影部分的面积.
如图,两个直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,平移距离为AE的长度,其中HG=20cm,QC=5cm,QG=8cm,求阴影部分的面积.