题目内容
如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
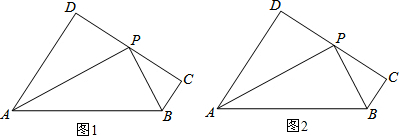
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?

考点:角平分线的性质,全等三角形的判定与性质
专题:
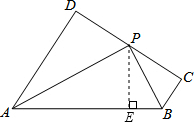
分析:(1)过点P作PE⊥AB于E,根据平行线的性质求出∠C=90°,即PC⊥BC,再根据角平分线上的点到角的两边距离相等可得PD=PE,PC=PE,从而得到PC=PD,然后根据线段中点的定义解答;
(2)过点P作PE⊥AB于E,根据平行线的性质求出∠C=90°,即PC⊥BC,利用AAS证明△PBE≌△PBC,得出∠EPB=∠CPB=35°,PE=PC,由PC=PD,等量代换得到PD=PE,再根据HL证明Rt△PAD≌Rt△PAE,得出∠APD=∠APE=55°,那么∠PAD=90°-∠APD=35°.
(2)过点P作PE⊥AB于E,根据平行线的性质求出∠C=90°,即PC⊥BC,利用AAS证明△PBE≌△PBC,得出∠EPB=∠CPB=35°,PE=PC,由PC=PD,等量代换得到PD=PE,再根据HL证明Rt△PAD≌Rt△PAE,得出∠APD=∠APE=55°,那么∠PAD=90°-∠APD=35°.
解答:
 解:(1)点P是线段CD的中点.理由如下:
解:(1)点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC.
 在△PBE与△PBC中,
在△PBE与△PBC中,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°-2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°-∠APD=35°.
 解:(1)点P是线段CD的中点.理由如下:
解:(1)点P是线段CD的中点.理由如下:过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC.
 在△PBE与△PBC中,
在△PBE与△PBC中,
|
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
|
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°-2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°-∠APD=35°.
点评:本题考查了角平分线的性质,全等三角形的判定与性质,平行线的性质,熟记性质并作出辅助线是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
有理数
的相反数是( )
| 1 |
| 2 |
| A、2 | ||
B、
| ||
C、-
| ||
| D、-2 |
学校以年线为单位开展广播操比赛,全年级有13个班级,每个班级有50名学生,规定班抽25名学生参加比赛,这时样本容量是( )
| A、13 | B、50 |
| C、325 | D、650 |
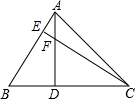 △ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )
△ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )| A、40° | B、45° |
| C、50° | D、60° |
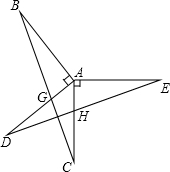 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H. 如图,AD=AC,AB=AE,∠DAB=∠CAE.
如图,AD=AC,AB=AE,∠DAB=∠CAE.