题目内容
反比例函数y=
中两个变量x,y的乘积不变,由此带来反比例函数的一些特性,如图①,P(x,y)是反比例函数y=
(k<0)的图象上的一个动点,PA⊥x轴,垂足为A,PB⊥y轴,垂足为B,则PA=|y|.PB=|x|,所以S矩形OAPB=PA•PB=|xy|=|k|,即矩形OAPB的面积不变,当k>0时上述结论也成立,我们可称这一性质为“反比例函数的面积不变性”,连接OP,此时,△PAO的面积为
|k|,也是定值,试利用“反比例函数的面积不变性”解决下列问题:
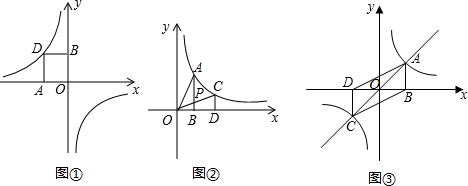
如图②、③,点A在反比例函数y=
的图象上,AB⊥x轴,垂足为B,
(1)如图②,点A在反比例函数y=
的图象上,CD⊥y轴,垂足为D,AB,CO相交于点P,试比较下列图形面积的大小
SRt△ABO SRt△CDO•S△APO S四边形BDCP(选填”>“”<“或”“=“)
(2)如图③,AO的延长线与反比例函数y=
的图象的另一个交点为C,CD⊥x轴,垂足为D,连接AD,BC,则四边形ABCD的面积为 .
| k |
| x |
| k |
| x |
| 1 |
| 2 |

如图②、③,点A在反比例函数y=
| 1 |
| x |
(1)如图②,点A在反比例函数y=
| 1 |
| x |
SRt△ABO
(2)如图③,AO的延长线与反比例函数y=
| 1 |
| x |
考点:反比例函数系数k的几何意义
专题:探究型
分析:(1)由反比例函数系数k的几何意义可得出△AOB和△COD的面积都等于
|k|,进而根据S△AOB-S△POB=S△COD-S△POB,即可得出S△APO=S四边形BDCP.
(2)先根据反比例函数与一次函数图象的特点求出AC两点的坐标特点,再根据反比例函数中系数k的几何意义求解即可.
| 1 |
| 2 |
(2)先根据反比例函数与一次函数图象的特点求出AC两点的坐标特点,再根据反比例函数中系数k的几何意义求解即可.
解答:
解:(1)由反比例函数系数k的几何意义可得,S△AOB=S△COD=
|k|.
∴S△AOB-S△POB=S△COD-S△POB,
∴S△APO=S四边形BDCP.
故答案为:=、=.
(2)∵反比例函数与一次函数图象关于原点对称,
∴AC两点关于原点对称,
∵反比例函数的解析式为:y=
,
∴S△AOB=S△OCD=S△AOD=S△BOC=
,
∴S四边形ABCD=S△AOB+S△OCD+S△AOD+S△BOC=2.
故答案为:2.
| 1 |
| 2 |
∴S△AOB-S△POB=S△COD-S△POB,
∴S△APO=S四边形BDCP.
故答案为:=、=.
(2)∵反比例函数与一次函数图象关于原点对称,
∴AC两点关于原点对称,
∵反比例函数的解析式为:y=
| 1 |
| x |
∴S△AOB=S△OCD=S△AOD=S△BOC=
| 1 |
| 2 |
∴S四边形ABCD=S△AOB+S△OCD+S△AOD+S△BOC=2.
故答案为:2.
点评:本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
在下列各数-(+3)、-22、(-2)2、(-1)2012、-|-4|中,负数有( )个.
| A、2个 | B、3个 | C、4个 | D、5个 |
下列方程变形错误的是( )
A、由方程
| ||||
B、由方程
| ||||
C、由方程
| ||||
D、由方程x-
|
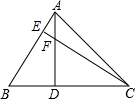 △ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )
△ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )| A、40° | B、45° |
| C、50° | D、60° |
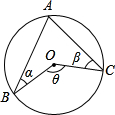 如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )
如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )| A、θ=α+β |
| B、θ+α+β=360° |
| C、θ+α+β=180° |
| D、θ=2α+2β |
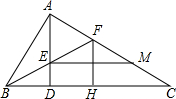 已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.
已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.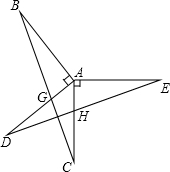 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.