题目内容
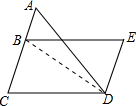 如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中,
如图所示,BC=DE,BE=DC,求证:(1)BC∥DE;(2)∠A=∠ADE.小明是这样想的,请你给小明的每个想法填上依据.连结BD,在△BCD和△DEB中,
|
考点:全等三角形的判定与性质
专题:推理填空题
分析:根据SSS证明△BCD≌△DEB,再根据全等三角形的性质得出∠CBD=∠EDB,最后利用平行线的判定和性质解答即可.
解答:
解:∵在△BCD和△DEB中,
∴△BCD≌△DEB(SSS)
∴∠CBD=∠EDB(全等三角形对应角相等)
∴BC∥DE(内错角相等,两直线平行)
∴∠A=∠ADE(两直线平行.内错角相等)
故答案为:SSS;全等三角形对应角相等; 内错角相等,两直线平行;两直线平行,内错角相等.
|
∴△BCD≌△DEB(SSS)
∴∠CBD=∠EDB(全等三角形对应角相等)
∴BC∥DE(内错角相等,两直线平行)
∴∠A=∠ADE(两直线平行.内错角相等)
故答案为:SSS;全等三角形对应角相等; 内错角相等,两直线平行;两直线平行,内错角相等.
点评:本题主要考查了平行线的判定和性质及全等三角形的判定与性质,属于基础题型,比较简单.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
有理数
的相反数是( )
| 1 |
| 2 |
| A、2 | ||
B、
| ||
C、-
| ||
| D、-2 |
学校以年线为单位开展广播操比赛,全年级有13个班级,每个班级有50名学生,规定班抽25名学生参加比赛,这时样本容量是( )
| A、13 | B、50 |
| C、325 | D、650 |
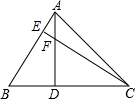 △ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )
△ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )| A、40° | B、45° |
| C、50° | D、60° |
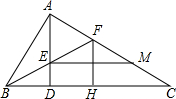 已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.
已知,△ABC中,∠BAC=90°,AD是高,BF平分∠ABC交AD于点E,交AC于F,作FH⊥BC,EM∥BC,写出图中所有与AF相等的线段,并证明.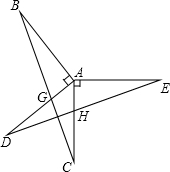 如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.
如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.