题目内容
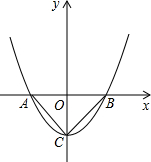 抛物线y=2x2-m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.
抛物线y=2x2-m与x轴并于A、B两点,与y轴交于点C,若∠ACB=90°,求抛物线的解析式.考点:抛物线与x轴的交点
专题:
分析:由条件可用m表示出A、B、C的坐标,再由条件可得到OA=OB=OC,可求得m的值,可求得抛物线解析式.
解答:
解:∵抛物线与x轴交于点A、B,与y轴交于点C,
∴A(-
,0),B(
,0),C(0,-m),
又∵∠ACB=90°,且y轴是抛物线的对称轴,
∴△ABC是等腰直角三角形,
∴OA=OB=OC,
∴
=m,即
=m2,解得m=0(不合题意,舍去)或m=
,
∴y=2x2-
.
∴A(-
|
|
又∵∠ACB=90°,且y轴是抛物线的对称轴,
∴△ABC是等腰直角三角形,
∴OA=OB=OC,
∴
|
| m |
| 2 |
| 1 |
| 2 |
∴y=2x2-
| 1 |
| 2 |
点评:本题主要考查待定系数法求函数解析式,利用抛物线与x轴的交点及等腰三角形的性质得到关于m的方程是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
有理数
的相反数是( )
| 1 |
| 2 |
| A、2 | ||
B、
| ||
C、-
| ||
| D、-2 |
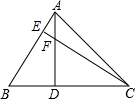 △ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )
△ABC中,AD⊥BC于D,CE⊥AB于E,CE与AD交于F.若CF=AB,则∠ACB的度数是( )| A、40° | B、45° |
| C、50° | D、60° |
一个事件发生的概率不可能是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
 如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )
如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )| A、70° | B、60° |
| C、55° | D、45° |