题目内容
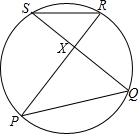已知P、Q、R、S在圆上，PR与QS相交于X，三角形RSX的面积为1.2，PX=3SX．则三角形PQX的面积为考点：圆周角定理,相似三角形的判定与性质
专题：
分析：根据同弧所对的圆周角相等，利用相似的判定方法可得出△SRX与△PQX相似，再根据相似三角形的面积之比等于相似比的平方即可得出答案．
解答：
解：∵∠S=∠P，∠R=∠Q，
∴△SRX∽△PQX，
∴
=（
）2，
∵PX=3SX，
∴
=
，
∴
=
，
∵S△RSX=1.2，
∴S△PQX=1.2×9=10.8，
故答案为10.8．
∴△SRX∽△PQX，
∴
| SSRX |
| SPQX |
| SX |
| PX |
∵PX=3SX，
∴
| SX |
| PX |
| 1 |
| 3 |
∴
| SSRX |
| SPQX |
| 1 |
| 9 |
∵S△RSX=1.2，
∴S△PQX=1.2×9=10.8，
故答案为10.8．
点评：本题考查了圆周角定理，以及等腰三角形的性质，掌握同弧所对的圆周角是圆心角的一半是解题的关键．
练习册系列答案
相关题目
学校以年线为单位开展广播操比赛，全年级有13个班级，每个班级有50名学生，规定班抽25名学生参加比赛，这时样本容量是（ ）
| A、13 | B、50 |
| C、325 | D、650 |
如图，AD=AC，AB=AE，∠DAB=∠CAE．
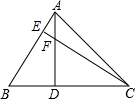△ABC中，AD⊥BC于D，CE⊥AB于E，CE与AD交于F．若CF=AB，则∠ACB的度数是（ ）| A、40° | B、45° |
| C、50° | D、60° |
如图，△ACB是等腰直角三角形，AC=BC，做射线CP，使∠ACP=20°，点A关于CP的对称点是D，连接AD交CP于点F，连接BD交CP于点E．一个事件发生的概率不可能是（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
如图，半径为5的⊙A中，弦BC、ED所对的圆心角分别是∠BAC，∠EAD，已知DE=6，∠BAC+∠EAD=180°．求点A到弦BC的距离．