题目内容
 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.(1)如图①,若点C在线段AB上,且AC=6,求线段MN的长;
(2)若点C是线段AB上任一点,其他条件不变,能求出线段MN的长度吗?请说明理由;
(3)若点C在线段AB外,M、N仍分别是AC、BC的中点,你能猜想MN的长度吗?请在备用图②、③中画出相应的图形,写出你的结论,并说明理由.
考点:两点间的距离
专题:
分析:(1)根据AB=10,AC=6求出BC的长,再根据M是线段AC的中点,N是线段BC的中点即可得出MC及NB的长,根据MN=MC+NB即可得出结论;
(2)根据(1)的方法求出MN=
AB;
(3)分点C在线段AB的延长线上与在AB的反向延长线上两种情况进行讨论.
(2)根据(1)的方法求出MN=
| 1 |
| 2 |
(3)分点C在线段AB的延长线上与在AB的反向延长线上两种情况进行讨论.
解答:解:(1)∵AB=10,AC=6,
∴BC=10-6=4.
∵M是线段AC的中点,N是线段BC的中点,
∴MC=
AC=3,NB=
BC=2,
∴MN=MC+NB=3+2=5;
(2)∵M是线段AC的中点,N是线段BC的中点,
∴MC=
AC,NB=
BC,
∴MN=MC+NB=
(AC+BC)=
AB=5;
(3)MN=5.
当点C在线段AB的延长线上时,
如图②,由图知MN=MC-NC
=
AC-
BC
=
(AC-BC)
=
AB
=5;
当点C在AB的反向延长线上时,
由图知MN=CN-CM
=
BC-
AC
=
(BC-AC)
=
AB
=5.
∴BC=10-6=4.
∵M是线段AC的中点,N是线段BC的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NB=3+2=5;
(2)∵M是线段AC的中点,N是线段BC的中点,
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)MN=5.
当点C在线段AB的延长线上时,

如图②,由图知MN=MC-NC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |

=5;
当点C在AB的反向延长线上时,
由图知MN=CN-CM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=5.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线y=-x2-2x+3与坐标轴的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
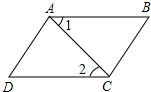 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
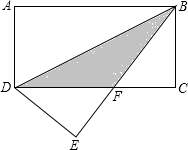 如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.
如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.
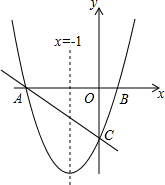 如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0). 如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.
如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.