题目内容
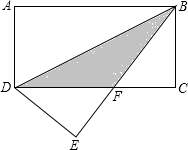 如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.
如图,将长方形ABCD沿BD对折,点A落在点E处,BE与CD相交于点F,若AD=3,BF=5.(1)求证:△DEF≌△BCF;
(2)求重叠部分的面积.
考点:翻折变换(折叠问题),全等三角形的判定与性质
专题:
分析:(1)证明∠E=∠C=90°,DE=BC,此为解决问题的关键性结论.运用AAS定理即可解决问题.
(2)运用(1)中的结论,求出DF=BF=5,即可解决问题.
(2)运用(1)中的结论,求出DF=BF=5,即可解决问题.
解答: 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AD=BC;
由翻折变换的性质知:∠E=∠A=90°,DE=AD,
∴∠E=∠C=90°,DE=BC;
在△DEF与△BCF中,
,
∴△DEF≌△BCF(AAS).
(2)∵△DEF≌△BCF,
∴DF=BF=5,
∴重叠部分的面积=
DF•AD=×5×3=7.5,
即重叠部分的面积为7.5.
 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,∴∠A=∠C=90°,AD=BC;
由翻折变换的性质知:∠E=∠A=90°,DE=AD,
∴∠E=∠C=90°,DE=BC;
在△DEF与△BCF中,
|
∴△DEF≌△BCF(AAS).
(2)∵△DEF≌△BCF,
∴DF=BF=5,
∴重叠部分的面积=
| 1 |
| 2 |
即重叠部分的面积为7.5.
点评:该题主要考查了翻折变换的性质、全等三角形的判定及其性质等几何知识点的应用问题;牢固掌握定理是基础、科学解答论证是关键.

练习册系列答案
相关题目
 如图,点G是线段EF的中点,则EG=
如图,点G是线段EF的中点,则EG= 如图,∠ABD=∠BCD=90°,BC=6,CD=8,当AB=
如图,∠ABD=∠BCD=90°,BC=6,CD=8,当AB=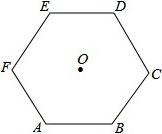 如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.
如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.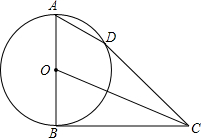 如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由. 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.