题目内容
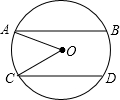 如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.
如图,在⊙O中,弦AB∥弦CD,且AB,CD位于圆心O的两侧,AB=8,CD=6,AB,CD之间的距离为7,连接OA,OC.(1)求⊙O的半径;
(2)过点A作⊙O的切线,交DC的延长线于点E,求线段CE的长.
考点:垂径定理,勾股定理
专题:计算题
分析:(1)作OM⊥AB于E,交CD与N,如图,设⊙O的半径为r,根据平行线的性质得ON⊥CD,则利用垂径定理得到AM=
AB=4,CN=
CD=3,根据平行线间的距离得到MN=7,接着根据勾股定理得OM2+42=r2①,ON2+32=r2②,利用②-①得ON2-OM2=7,加上OM+On=7可解得ON=4,OM=3,则OA=
=5;
(2)作AH⊥CD于H,连结OE,如图,则AH=MN=7,易得Rt△OAM≌Rt△CON,则∠AOM=∠OCN,于是可证得∠AOM+∠CON=90°,则OA⊥OC,再根据切线的性质得OA⊥AE,所以
OC∥AE,根据平行线的性质有OCN=∠AEM,于是可判断△OCN∽△AEH,利用相似比计算出EH=
,加上HC=HN-CN=4-3=1,所以EC=EH+HC=
.
| 1 |
| 2 |
| 1 |
| 2 |
| AM2+OM2 |
(2)作AH⊥CD于H,连结OE,如图,则AH=MN=7,易得Rt△OAM≌Rt△CON,则∠AOM=∠OCN,于是可证得∠AOM+∠CON=90°,则OA⊥OC,再根据切线的性质得OA⊥AE,所以
OC∥AE,根据平行线的性质有OCN=∠AEM,于是可判断△OCN∽△AEH,利用相似比计算出EH=
| 21 |
| 4 |
| 25 |
| 4 |
解答:解:(1)作OM⊥AB于E,交CD与N,如图,设⊙O的半径为r,
∵AB∥CD,
∴ON⊥CD,
∴AM=
AB=4,CN=
CD=3,MN=7,
在Rt△AOM中,∵OM2+AM2=OA2,
∴OM2+42=r2①,
在Rt△CON中,∵ON2+CN2=OC2,
∴ON2+32=r2②,
②-①得ON2-OM2=7,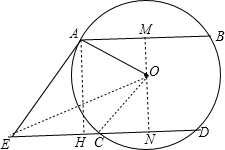
∴(ON+OM)(ON-OM)=7,
∴ON-OM=1,
∴ON=4,OM=3,
∴OA=
=5,
即⊙O的半径为5;
(2)作AH⊥CD于H,连结OE,如图,则AH=MN=7,
在Rt△OAM和Rt△CON中
,
∴Rt△OAM≌Rt△CON,
∴∠AOM=∠OCN,
∵∠AOM+∠CON=90°,
∴∠AOM+∠CON=90°,
∴OA⊥OC,
∵AE为切线,
∴OA⊥AE,
∴OC∥AE,
∴∠OCN=∠AEM,
∴△OCN∽△AEH,
∴
=
,即
=
,解得EH=
,
∵HN=AM=4,
∴HC=HN-CN=4-3=1,
∴EC=EH+HC=
+1=
.
∵AB∥CD,
∴ON⊥CD,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOM中,∵OM2+AM2=OA2,
∴OM2+42=r2①,
在Rt△CON中,∵ON2+CN2=OC2,
∴ON2+32=r2②,
②-①得ON2-OM2=7,

∴(ON+OM)(ON-OM)=7,
∴ON-OM=1,
∴ON=4,OM=3,
∴OA=
| AM2+OM2 |
即⊙O的半径为5;
(2)作AH⊥CD于H,连结OE,如图,则AH=MN=7,
在Rt△OAM和Rt△CON中
|
∴Rt△OAM≌Rt△CON,
∴∠AOM=∠OCN,
∵∠AOM+∠CON=90°,
∴∠AOM+∠CON=90°,
∴OA⊥OC,
∵AE为切线,
∴OA⊥AE,
∴OC∥AE,
∴∠OCN=∠AEM,
∴△OCN∽△AEH,
∴
| CN |
| EH |
| ON |
| AH |
| 3 |
| EH |
| 4 |
| 7 |
| 21 |
| 4 |
∵HN=AM=4,
∴HC=HN-CN=4-3=1,
∴EC=EH+HC=
| 21 |
| 4 |
| 25 |
| 4 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、切线的性质和三角形全等的判定与性质.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )
如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )| A、15cm | B、18cm |
| C、20cm | D、22cm |
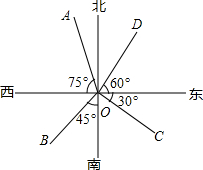 如图所示,对图中各射线表示的方向下列判断错误的是( )
如图所示,对图中各射线表示的方向下列判断错误的是( )| A、射线OA的方向是北偏西15° |
| B、射线OB的方向是南偏西45° |
| C、射线OC的方向是南偏东60° |
| D、射线OD的方向是北偏东60° |
在某次实验中,测得两个变量m和v之间的4组对应数据如下表
则m与V之间的关系最接近于下列各关系式中的是( )
| m | 1 | 2 | 3 | 4 |
| V | 0.01 | 2.90 | 8.02 | 15.10 |
| A、v=m2-1 |
| B、v=2 m |
| C、v=3 m-1 |
| D、v=3 m+1 |
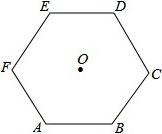 如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.
如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S. 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点. 两条直线l1,l2相交于一点,
两条直线l1,l2相交于一点,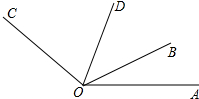 如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数.
如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数. △ABC中,F是BC中点,D在AC上,
△ABC中,F是BC中点,D在AC上,