题目内容
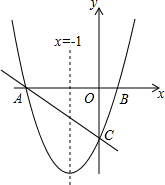 如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
如图,抛物线y=ax2+bx+c的对称轴为x=-1,抛物线与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).(1)求点B的坐标;
(2)若点P在抛物线上,a=1,且S△POC=4S△BOC,求点P的坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)由二次函数的对称性可知,点B、C到对称轴的距离相等可求得B点的坐标;
(2)由条件可先求得抛物线的解析式,再求得△BOC的面积,结合条件可求得P点到y轴的距离,即P点的横坐标,代入可求得P点坐标.
(2)由条件可先求得抛物线的解析式,再求得△BOC的面积,结合条件可求得P点到y轴的距离,即P点的横坐标,代入可求得P点坐标.
解答:解:(1)∵对称轴为x=-1,A点坐标为(-3,0),
∴B点坐标为(1,0);
(2)由条件其对称轴为x=-1,即-
=-1,
当a=1时,代入可求得b=2,
∴抛物线为y=x2+2x+c,
又∵过B(1,0),代入可求得c=-3,
∴抛物线解析式为y=x2+2x-3,
∴C点坐标为(0,-3),
∴OC=3,且OB=1,
∴S△BOC=
OB•OC=
×3×1=
,
∴S△POC=4S△BOC=6,
设P到x轴的距离为h,则S△POC=
OC•h=
h=6,解得h=4,
∴P点的横坐标为4或-4,
当x=4时,代入抛物线解析式可求得y=21,
当x=-4时,代入抛物线解析式可求得y=5,
∴P点坐标为(4,21)或(-4,5).
∴B点坐标为(1,0);
(2)由条件其对称轴为x=-1,即-
| b |
| 2a |
当a=1时,代入可求得b=2,
∴抛物线为y=x2+2x+c,
又∵过B(1,0),代入可求得c=-3,
∴抛物线解析式为y=x2+2x-3,
∴C点坐标为(0,-3),
∴OC=3,且OB=1,
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴S△POC=4S△BOC=6,
设P到x轴的距离为h,则S△POC=
| 1 |
| 2 |
| 3 |
| 2 |
∴P点的横坐标为4或-4,
当x=4时,代入抛物线解析式可求得y=21,
当x=-4时,代入抛物线解析式可求得y=5,
∴P点坐标为(4,21)或(-4,5).
点评:本题主要考查待定系数法求二次函数解析式及与坐标轴的交点,利用二次函数的对称性求得B点的坐标、求得二次函数的解析式是解题的关键.

练习册系列答案
相关题目
 如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )
如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )| A、15cm | B、18cm |
| C、20cm | D、22cm |
 已知,点G是△ABC的重心,AG⊥GC,AG=3,GC=4,求BG的长度.
已知,点G是△ABC的重心,AG⊥GC,AG=3,GC=4,求BG的长度. 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点. 两条直线l1,l2相交于一点,
两条直线l1,l2相交于一点,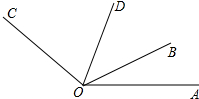 如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数.
如图,∠BOC=4∠AOB,OD是∠AOC的平分线,∠BOD=42°,求∠AOB的度数.