题目内容
已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边做正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC-CD.
(2)如图2,当点D在线段BC的延长线时,其它条件不变,请写出CF、BC、CD三条线段之间的关系,并证明你的结论.
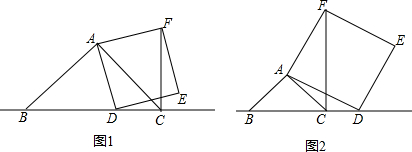
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC-CD.
(2)如图2,当点D在线段BC的延长线时,其它条件不变,请写出CF、BC、CD三条线段之间的关系,并证明你的结论.

考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:(1)①根据正方形得性质得∠DAE=90°,AD=AE,再利用等角的余角相等得到∠BAD=∠CAF,于是可根据“SAS”证明△ABD≌△ACF,则∠ABD=∠ACF,利用∠ABD+∠ACB=90°,得到∠ACF+∠ACB=90°,则根据垂直的定义得到BD⊥CF;
②根据三角形全等的性质得BD=CF,然后利用BD=BC-CD即可得到结论;
(2)与(1)中的证明方法一样可得△ABD≌△ACF,则BD=CF,由于BD=BC+CD,所以CF=BC+CD.
②根据三角形全等的性质得BD=CF,然后利用BD=BC-CD即可得到结论;
(2)与(1)中的证明方法一样可得△ABD≌△ACF,则BD=CF,由于BD=BC+CD,所以CF=BC+CD.
解答:解:(1)①∵四边形ADEF为正方形,
∴∠DAE=90°,AD=AE,
即∠DAC+∠CAF=90°,
∵∠BAC=90°,即∠BAD+∠DAC=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴∠ABD=∠ACF,
∵∠ABD+∠ACB=90°,
∴∠ACF+∠ACB=90°,
即∠DCF=90°,
∴BD⊥CF;
②∵△ABD≌△ACF,
∴BD=CF,
而BD=BC-CD,
∴CF=BC-CD;
(2)CF=BC+CD.理由如下:
与(1)中的证明方法一样可得△ABD≌△ACF,
∴BD=CF,
而BD=BC+CD,
∴CF=BC+CD.
∴∠DAE=90°,AD=AE,
即∠DAC+∠CAF=90°,
∵∠BAC=90°,即∠BAD+∠DAC=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
|
∴△ABD≌△ACF(SAS),
∴∠ABD=∠ACF,
∵∠ABD+∠ACB=90°,
∴∠ACF+∠ACB=90°,
即∠DCF=90°,
∴BD⊥CF;
②∵△ABD≌△ACF,
∴BD=CF,
而BD=BC-CD,
∴CF=BC-CD;
(2)CF=BC+CD.理由如下:
与(1)中的证明方法一样可得△ABD≌△ACF,
∴BD=CF,
而BD=BC+CD,
∴CF=BC+CD.
点评:本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形得性质.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )
如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边与点D,交AC边于点E,若AE=4cm,则△ABD的周长为( )| A、15cm | B、18cm |
| C、20cm | D、22cm |
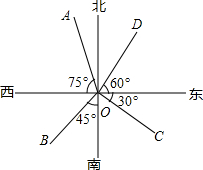 如图所示,对图中各射线表示的方向下列判断错误的是( )
如图所示,对图中各射线表示的方向下列判断错误的是( )| A、射线OA的方向是北偏西15° |
| B、射线OB的方向是南偏西45° |
| C、射线OC的方向是南偏东60° |
| D、射线OD的方向是北偏东60° |
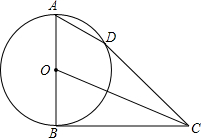 如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.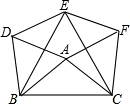 如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC. 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点. 如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.
如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.