题目内容
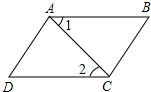 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:平行线的判定与性质
专题:
分析:由条件可证明AB∥DC,结合角相等可得到∠DAC=∠BCA,可证明AD∥BC,再利用平行线的性质可求得∠B=∠D,可得出答案.
解答:解:∵∠1=∠2,
∴AB∥CD,
∴①正确;
∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2,
即∠DAC=∠BCA,
∴AD∥BC,
∴②正确;
∴∠D+∠DAB=∠B+∠DAB=180°,
∴∠B=∠D,
∴③正确;
只有当AB=AC时才会有∠B=∠ACB=∠D,
∴④不正确;
综上可知正确的有三个,
故选C.
∴AB∥CD,
∴①正确;
∵∠BAD=∠BCD,
∴∠BAD-∠1=∠BCD-∠2,
即∠DAC=∠BCA,
∴AD∥BC,
∴②正确;
∴∠D+∠DAB=∠B+∠DAB=180°,
∴∠B=∠D,
∴③正确;
只有当AB=AC时才会有∠B=∠ACB=∠D,
∴④不正确;
综上可知正确的有三个,
故选C.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行.

练习册系列答案
相关题目
在某次实验中,测得两个变量m和v之间的4组对应数据如下表
则m与V之间的关系最接近于下列各关系式中的是( )
| m | 1 | 2 | 3 | 4 |
| V | 0.01 | 2.90 | 8.02 | 15.10 |
| A、v=m2-1 |
| B、v=2 m |
| C、v=3 m-1 |
| D、v=3 m+1 |
把160000用科学记数法表示为( )
| A、16×104 |
| B、1.6×104 |
| C、1.6×105 |
| D、0.16×104 |
 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点. 如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值.
如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止.设运动时间为t秒,当以B,D,E为顶点的三角形与△ABC相似时,求t的值. 如图,五边形ABCDE是正五边形,点P在直线AB上运动当点P与正五边形的至少两个顶点的距离相等时,警报器会发出警报,在直线AB上会发出警报的点有( )个.
如图,五边形ABCDE是正五边形,点P在直线AB上运动当点P与正五边形的至少两个顶点的距离相等时,警报器会发出警报,在直线AB上会发出警报的点有( )个. △ABC中,F是BC中点,D在AC上,
△ABC中,F是BC中点,D在AC上, 如图,菱形ABCD中,对角线AC与BD相交于O,过A作AE∥BD,过O作OE∥AB,OE与AE相交于E,请问,四边形AODE是什么特殊的四边形?并证明你的结论.
如图,菱形ABCD中,对角线AC与BD相交于O,过A作AE∥BD,过O作OE∥AB,OE与AE相交于E,请问,四边形AODE是什么特殊的四边形?并证明你的结论.