题目内容
抛物线y=-x2-2x+3与坐标轴的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:抛物线与x轴的交点
专题:
分析:令y=0得到关于x的一元二次方程,看其判别式的符号即可判断抛物线与x轴的交点个数,又与y轴有一个交点,可得到答案.
解答:解:
在y=-x2-2x+3中令y=0可得x2+2x-3=0,
其判别式△=4+12=16>0,
∴一元二次方程有两个不相等的实数根,
∴抛物线与x轴有两个交点,
又抛物线与y轴一定有一个交点,
∴抛物线y=-x2-2x+3与坐标轴有三个交点,
故选D.
在y=-x2-2x+3中令y=0可得x2+2x-3=0,
其判别式△=4+12=16>0,
∴一元二次方程有两个不相等的实数根,
∴抛物线与x轴有两个交点,
又抛物线与y轴一定有一个交点,
∴抛物线y=-x2-2x+3与坐标轴有三个交点,
故选D.
点评:本题主要考查二次函数与坐标轴的交点,掌握二次函数与x轴的交点横坐标是对应一元二次方程的解是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
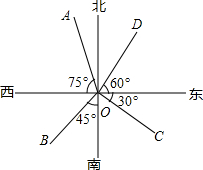 如图所示,对图中各射线表示的方向下列判断错误的是( )
如图所示,对图中各射线表示的方向下列判断错误的是( )| A、射线OA的方向是北偏西15° |
| B、射线OB的方向是南偏西45° |
| C、射线OC的方向是南偏东60° |
| D、射线OD的方向是北偏东60° |
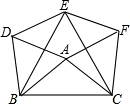 如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC. 已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点.
已知:点A、B、C在直线l上,线段AB=10,M是线段AC的中点,N是线段BC的中点. 如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
如图,OP是直角∠MON的平分线,以O为圆心,1为半径作
 如图,五边形ABCDE是正五边形,点P在直线AB上运动当点P与正五边形的至少两个顶点的距离相等时,警报器会发出警报,在直线AB上会发出警报的点有( )个.
如图,五边形ABCDE是正五边形,点P在直线AB上运动当点P与正五边形的至少两个顶点的距离相等时,警报器会发出警报,在直线AB上会发出警报的点有( )个.