题目内容
17.已知(x-1)|x|-1有意义且恒等于1,则x的值为( )| A. | ±1 | B. | 1 | C. | -1 | D. | 2 |
分析 根据(x-1)|x|-1≡1,可得$\left\{\begin{array}{l}{|x|-1=0}\\{x-1≠0}\end{array}\right.$、x-1=1或$\left\{\begin{array}{l}{x-1=-1}\\{|x|-1=2n(n是整数)}\end{array}\right.$,据此求出x的值为多少即可.
解答 解:∵(x-1)|x|-1≡1,
∴$\left\{\begin{array}{l}{|x|-1=0}\\{x-1≠0}\end{array}\right.$、x-1=1或$\left\{\begin{array}{l}{x-1=-1}\\{|x|-1=2n(n是整数)}\end{array}\right.$,
由$\left\{\begin{array}{l}{|x|-1=0}\\{x-1≠0}\end{array}\right.$,
解得x=-1;
由x-1=1,
解得x=2;
当$\left\{\begin{array}{l}{x-1=-1}\\{|x|-1=2n(n是整数)}\end{array}\right.$时,
x无解.
综上,可得
x的值为-1或2.
故选:C、D.
点评 此题主要考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:(1)a0=1(a≠0);(2)00≠1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.解分式方程$\frac{2}{x+1}+\frac{3}{x-1}=\frac{6}{{{x^2}-1}}$,分以下四步,其中,错误的一步是( )
| A. | 方程两边分式的最简公分母是(x-1)(x+1) | |
| B. | 方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6 | |
| C. | 解这个整式方程,得x=1 | |
| D. | 原方程的解为x=1 |
5.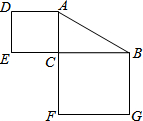 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 225 | B. | 200 | C. | 250 | D. | 150 |
6.在计算结果为a6的个数是( )
| A. | a2•a3 | B. | a12÷a2 | C. | (-a2)3 | D. | a4•a2 |
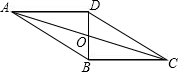 如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,BD⊥AD,AD=6,AB=10,求DC,BC及平行四边形ABCD的面积?
如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,BD⊥AD,AD=6,AB=10,求DC,BC及平行四边形ABCD的面积?