题目内容
9.①比较大小:2$\sqrt{3}$< $\sqrt{13}$;②计算:$\sqrt{2xy}$-$\sqrt{8y}$;
③化简:$\sqrt{(2-\sqrt{5})^{2}}$=$\sqrt{5}-2$;
④已知:y=$\sqrt{x-2}$+$\sqrt{2-x}$+5,则$\frac{x}{y}$=$\frac{2}{5}$.
分析 ①首先求出两个数的平方是多少,然后比较出两个数的平方的大小,即可判断出两个数的大小关系;
②首先化简每个二次根式,然后求出算式的值是多少即可;
③一个数的算术平方根大于或等于0,进而求出算式的值是多少即可;
④首先根据二次根式有意义的条件,可得x-2=0,据此求出x的值是多少,进而求出y的值是多少;然后用x除以y,求出$\frac{x}{y}$等于多少即可.
解答 解:①${(2\sqrt{3})}^{2}=12{,(\sqrt{13})}^{2}=13$,
∵12<13,
∴$2\sqrt{3}<\sqrt{13}$.
②$\sqrt{2xy}$-$\sqrt{8y}$
=$\sqrt{2y}•\sqrt{x}-2\sqrt{2y}$
=$\sqrt{2y}(\sqrt{x}-2)$
③$\sqrt{(2-\sqrt{5})^{2}}$=$\sqrt{5}-2$
④∵x-2≥0,2-x≥0,
∴x-2=0,
∴x=2,y=0+0+5=5,
∴$\frac{x}{y}$=$\frac{2}{5}$
故答案为:<、$\sqrt{5}-2、\frac{2}{5}$.
点评 (1)此题主要考查了实数大小的比较,以及二次根式的化简和二次根式的加减运算,要熟练掌握.
(2)此题还考查了一个数的算术平方根的求法,要熟练掌握,解答此题的关键是要明确:一个数的算术平方根大于或等于0.

练习册系列答案
相关题目
17.已知(x-1)|x|-1有意义且恒等于1,则x的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 2 |
4.-32的相反数是( )
| A. | 9 | B. | -9 | C. | 6 | D. | -6 |
1.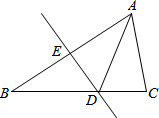 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
 如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD=10.
如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD=10. 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE,延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为$\frac{1}{2}$;③∠AEF=60°;④图中只有三对三角形全等;⑤DE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.其中正确的个数是( )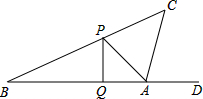 2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.