题目内容
19.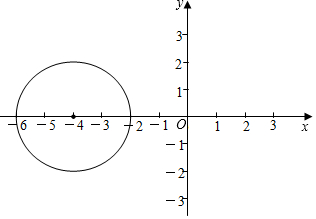 如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得
如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得⊙P1.
(1)画出⊙P1;
(2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A,B,求劣弧AB与弦AB围成的图形的面积(结果保留π).
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用扇形面积减去三角形面积进而得出答案.
解答  解:(1)如图所示:⊙P1,即为所求;
解:(1)如图所示:⊙P1,即为所求;
(2)如图所示:劣弧AB与弦AB围成的图形的面积为:$\frac{90π×{2}^{2}}{360}$-$\frac{1}{2}$×2×2=π-2.
点评 此题主要考查了平移变换以及扇形面积求法,正确掌握扇形面积求法是解题关键.

练习册系列答案
相关题目
10.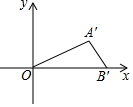 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )| A. | (2,1) | B. | (8,4) | C. | (2,1)或(-2,-1) | D. | (8,4)或(-8,-4) |
8. 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
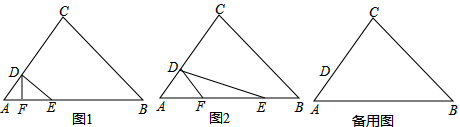
 已知正方形的边长是x厘米,那么阴影部分的面积可以表示为$\frac{1}{8}$πx2平方厘米.如果x=10,计算阴影部分的面积.
已知正方形的边长是x厘米,那么阴影部分的面积可以表示为$\frac{1}{8}$πx2平方厘米.如果x=10,计算阴影部分的面积.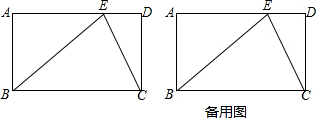
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,则图中标记为正方形A,B,C,D的面积之和为100cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,则图中标记为正方形A,B,C,D的面积之和为100cm2.