题目内容
3.计算(1)$\frac{{x}^{2}+1}{x-6}$•$\frac{{x}^{2}-36}{{x}^{3}+x}$
(2)$\frac{a+1}{a-1}$-$\frac{{{a^2}+a}}{{{a^2}-1}}$.
分析 先将分子分母因式分解,然后利用分式的基本性质即可求出答案.
解答 解:(1)原式=$\frac{{x}^{2}+1}{x-6}$•$\frac{(x+6)(x-6)}{x({x}^{2}+1)}$=$\frac{x+6}{x}$
(2)原式=$\frac{a+1}{a-1}$-$\frac{a(a+1)}{(a-1)(a+1)}$
=$\frac{a+1}{a-1}$-$\frac{a}{a-1}$
=$\frac{1}{a-1}$
点评 本题考查分式的混合运算,解题的关键是熟练运用因式分解以及分式的基本性质,本题属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题中:
(1)形状相同的两个三角形是全等形;
(2)在两个三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有( )
(1)形状相同的两个三角形是全等形;
(2)在两个三角形中,相等的角是对应角,相等的边是对应边;
(3)全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
8. 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
 如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )
如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=55°,则∠AOC=( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
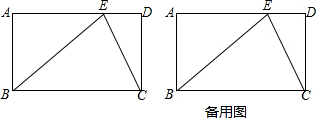
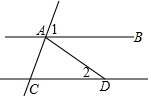 如图,已知直线AB∥CD,且线段AD=CD,若∠1=75°,则∠2的度数是30°.
如图,已知直线AB∥CD,且线段AD=CD,若∠1=75°,则∠2的度数是30°.