题目内容
2．
如图，若△AOB≌△COD，∠B=30°，∠AOC=52°，则∠CEO的度数为82°．
分析 根据全等三角形的性质得到∠D=∠B=30°，∠AOB=∠COD，然后又三角形的外角的性质即可得到结论．
解答 解：∵△AOB≌△COD，
∴∠D=∠B=30°，∠AOB=∠COD，
∴∠EOD=∠AOC=52°，
∴∠CEO=∠D+∠EOD=82°，
故答案为：82°．
点评 本题考查了全等三角形的性质，三角形的外角的性质，熟练掌握全等三角形的性质是解题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
12．
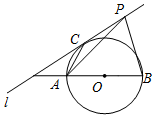如图，直线l与以线段AB为直径的圆相切于点C，AB=6，AC=3，点P是直线l上一个动点．当∠APB的度数最大时，线段BP的长度为（ ）
如图，直线l与以线段AB为直径的圆相切于点C，AB=6，AC=3，点P是直线l上一个动点．当∠APB的度数最大时，线段BP的长度为（ ）| A． | 6 | B． | $6\sqrt{3}$ | C． | 9 | D． | $3\sqrt{3}$ |
10．
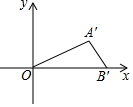如图，平面直角坐标系中，以原点O为位似中心，按相似比为1：2将△OAB放大后得到△OA′B′，若点A的对应点A′的坐标为（4，2），则点A的坐标为（ ）
如图，平面直角坐标系中，以原点O为位似中心，按相似比为1：2将△OAB放大后得到△OA′B′，若点A的对应点A′的坐标为（4，2），则点A的坐标为（ ）| A． | （2，1） | B． | （8，4） | C． | （2，1）或（-2，-1） | D． | （8，4）或（-8，-4） |
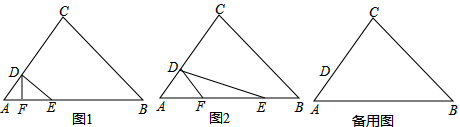
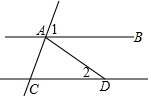如图，已知直线AB∥CD，且线段AD=CD，若∠1=75°，则∠2的度数是30°．