题目内容
1. 如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$.
如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$.(1)求△ABC的周长;
(2)求sin∠DAB的值.
分析 (1)在Rt△ADC中,由cos∠ADC=$\frac{3}{4}$、AD=5求得CD=3,根据勾股定理分别求得AC、AB,即可得答案;
(2)由AD=BD知∠DAB=∠B,从而由sin∠DAB=sinB可得答案.
解答 解:(1)在Rt△ADC中,∵cos∠ADC=$\frac{3}{4}$、AD=5,
∴CD=3,
∴AC=$\sqrt{A{D}^{2}-C{D}^{2}}$=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=4$\sqrt{5}$,
∴△ABC的周长为12+4$\sqrt{5}$;
(2)∵AD=BD,
∴∠DAB=∠B,
∴sin∠DAB=sinB=$\frac{AC}{AB}$=$\frac{4}{4\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查解直角三角形及等腰三角形的性质,熟练掌握勾股定理和三角函数的定义是解题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
12.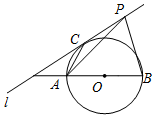 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $3\sqrt{3}$ |
10.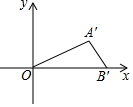 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
 如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )
如图,平面直角坐标系中,以原点O为位似中心,按相似比为1:2将△OAB放大后得到△OA′B′,若点A的对应点A′的坐标为(4,2),则点A的坐标为( )| A. | (2,1) | B. | (8,4) | C. | (2,1)或(-2,-1) | D. | (8,4)或(-8,-4) |
 在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法).
在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法). 如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠EOC=62°,求∠AOB的度数.
如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠EOC=62°,求∠AOB的度数.