题目内容
5. 如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 ①△BDC≌△CEB,根据等边对等角得:∠ABC=∠ACB,由高得:∠BDC=∠CEB=90°,所以利用AAS可证明全等;
②△BEO≌△CDO,加上对顶角相等,利用AAS可证明全等;
③△AEO≌△ADO,根据HL可证明全等;
④△ABF≌△ACF,根据SAS可证明全等;
⑤△BOF≌△COF,根据等腰三角形三线合一的性质得:BF=FC,∠AFB=∠AFC,利用SAS可证明全等;
⑥△AOB≌△AOC,根据SAS可证明全等;
⑦△ABD≌△ACE,利用AAS可证明全等.
解答 解:有7对全等三角形:
①△BDC≌△CEB,理由是:
∵AB=AC,
∴∠ABC=∠ACB,
∵BD和CE是两腰上的高,
∴∠BDC=∠CEB=90°,
在△BDC和△CEB中,
∵$\left\{\begin{array}{l}{∠BDC=∠CEB}\\{∠ACB=∠ABC}\\{BC=CB}\end{array}\right.$,
∴△BDC≌△CEB(AAS),
∴BE=DC,
②△BEO≌△CDO,理由是:
在△BEO和△CDO中,
∵$\left\{\begin{array}{l}{∠BEO=∠CDO}\\{∠BOE=∠COD}\\{BE=CD}\end{array}\right.$,
∴△BEO≌△CDO(AAS),
③△AEO≌△ADO,理由是:
由△BEO≌△CDO得:EO=DO,
在Rt△AEO和Rt△ADO中,
$\left\{\begin{array}{l}{AO=AO}\\{EO=OD}\end{array}\right.$,
∴Rt△AEO≌Rt△ADO(HL),
∴∠EAO=∠DAO,
④△ABF≌△ACF,理由是:
在△ABF和△ACF中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠EAO=∠DAO}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ACF(SAS),
⑤△BOF≌△COF,理由是:
∵AB=AC,∠BAF=∠CAF,
∴BF=FC,∠AFB=∠AFC,
在△BOF和△COF中,
∵$\left\{\begin{array}{l}{OF=OF}\\{∠AFB=∠ADC}\\{BF=FC}\end{array}\right.$,
∴△BOF≌△COF(SAS),
⑥△AOB≌△AOC,理由是:
在△AOB和△AOC中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAO}\\{AO=AO}\end{array}\right.$,
∴△AOB≌△AOC(SAS),
⑦△ABD≌△ACE,理由是:
在△ABD和△ACE中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{∠ADB=∠AEC=90°}\end{array}\right.$,
∴△ABD≌△ACE(AAS);
故选C.
点评 本题主要考查了三角形全等的性质和判定、等腰三角形的性质,熟练掌握三角形全等的判定方法是关键,要书写三角形全等时要按顺序书写,才能做到不重不漏.

| A. | $\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$ |
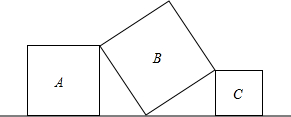 如图,将三个大小不同的正方形如图放置,顶点处两两相接.若正方形A的边长为5,正方形C的边长为3,则正方形B的面积为34.
如图,将三个大小不同的正方形如图放置,顶点处两两相接.若正方形A的边长为5,正方形C的边长为3,则正方形B的面积为34.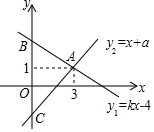 如图,一次函数y1=kx+4与y2=x+a的图象相交于点A(3,1),与y轴分别相交于点B、C两点.
如图,一次函数y1=kx+4与y2=x+a的图象相交于点A(3,1),与y轴分别相交于点B、C两点.