题目内容
15.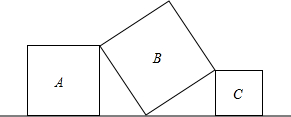 如图,将三个大小不同的正方形如图放置,顶点处两两相接.若正方形A的边长为5,正方形C的边长为3,则正方形B的面积为34.
如图,将三个大小不同的正方形如图放置,顶点处两两相接.若正方形A的边长为5,正方形C的边长为3,则正方形B的面积为34.
分析 证△DEF≌△FH,推出DE=FH=5,根据勾股定理求出FG即可.
解答 解:如图,∵根据正方形的性质得:DF=FG,∠DEF=∠GHF=∠DFG=90°,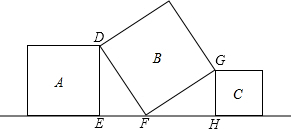
∴∠EDF+∠DFE=90°,∠DFE+∠GFH=90°,
∴∠EDF=∠GFH,
在△DEF和△FHG中
$\left\{\begin{array}{l}{∠DEF=∠FHG}\\{∠EDF=∠HFG}\\{DF=FG}\end{array}\right.$,
∴△DEF≌△FHG(AAS),
∴DE=FH=5,
∵GH=3,
∴在Rt△GHF中,由勾股定理得:FG=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$,
所以正方形B的面积为34.
故答案为34.
点评 本题考查了正方形性质,全等三角形的性质和判定,勾股定理的应用,解此题的关键是求出FH的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若圆锥的侧面展开图是个半圆,则该圆锥的侧面积与全面积之比为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.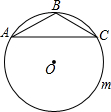 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
4.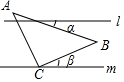 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.
如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积. 如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )