题目内容
14.先化简,再求值:$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$,其中x=$\frac{5}{3}$.分析 先把第1个分式的分子分母因式分解,再约分后进行同分母的减法运算,然后把x的值代入计算即可.
解答 解:原式=$\frac{(x+1)^{2}}{(x+1)(x-1)}$-$\frac{x}{x-1}$
=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$
=$\frac{1}{x-1}$,
当x=$\frac{5}{3}$时,
原式=$\frac{1}{\frac{5}{3}-1}$=$\frac{3}{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
4.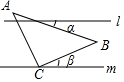 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
2.下列分式中,最简分式是( )
| A. | $\frac{2}{x-2}$ | B. | $\frac{2}{4x}$ | C. | $\frac{y-x}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-4x+4}{x-2}$ |
9.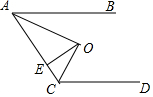 如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
 如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )| A. | 2 | B. | 4 | C. | 8 | D. | 无法确定 |
3. 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )
 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )| A. | a>b | B. | a>-b | C. | -a<-b | D. | a<b |
 如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )