题目内容
13.检修小组乘维修车从A地出发,在东西走向的路上检修线路,如果规定向东为正,向西为负,一天中每次行驶记录如下(单位:千米);-4,+7,-9,+8,+6,-4,-3.(1)收工时在A地的哪个方向?距A地多远?
(2)哪一次行驶后距A地最远?
(3)若每千米耗油0.3升,从出发到收工时共耗油多少升?
分析 (1)根据有理数的加法运算,可得答案;
(2)根据每次的绝对值,可得每次距A地的距离,根据有理数的大小比较,可得答案;
(3)根据行车的路程乘以单位耗油量,可得总耗油量.
解答 解:(1)-4+7-9+8+6-4-3=+1,
答:收工时在A地的东边,距A地1千米;
(2)第一次距A地|-4|=4千米;
第二次:|-4+7|=3千米;
第三次:|-4+7-9|=6千米;
第四次:|-4+7-9+8|=2千米;
第五次:|-4+7-9+8+6|=8千米;
第六次:|-4+7-9+8+6-4|=4千米;
第七次:|-4+7-9+8+6-4-3|=1千米,
8>6>4>3>2>1,
答:距A地最远的是第5次;
(3)|-4|+|+7|+|-9|+|+8|+|+6|+|-4|+|-3|=4+7+9+8+6+4+3=41(千米)
41×0.3=12.3(升).
答:从出发到收工时共耗油12.3升.
点评 此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.

练习册系列答案
相关题目
4.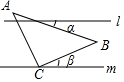 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
8.下列分式中,最简分式是( )
| A. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
18.三角形中,三个内角的比为1:3:6,它的三个外角的比为( )
| A. | 1:3:6 | B. | 6:3:1 | C. | 9:7:4 | D. | 3:5:2 |
2.下列分式中,最简分式是( )
| A. | $\frac{2}{x-2}$ | B. | $\frac{2}{4x}$ | C. | $\frac{y-x}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-4x+4}{x-2}$ |
3. 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )
 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )| A. | a>b | B. | a>-b | C. | -a<-b | D. | a<b |
 如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )