题目内容
已知C为直线AB上任一点,M、N分别为AC、BC的中点,试探究MN与AB之间的关系,并说明理由.


考点:两点间的距离
专题:
分析:分三种情况当C在线段AB上时,当C在线段AB的延长线上时,当C在线段BA的延长线上时,进行推论说明.
解答:解:∵M是线段AC的中点,∴CM=
AC,
∵N是线段BC的中点,∴CN=
BC,
以下分三种情况讨论,
当C在线段AB上时,MN=CM+CN=
AC+
BC=
(AC+BC)=
AB;

当C在线段AB的延长线上时,MN=CM-CN=
AC-
BC=
(AC-BC)=
AB;

当C在线段BA的延长线上时,MN=CN-CM=
BC-
AC=
(BC-AC)=
AB;

综上:MN=
AB.
故答案为:MN=
AB.
| 1 |
| 2 |
∵N是线段BC的中点,∴CN=
| 1 |
| 2 |
以下分三种情况讨论,
当C在线段AB上时,MN=CM+CN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

当C在线段AB的延长线上时,MN=CM-CN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

当C在线段BA的延长线上时,MN=CN-CM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

综上:MN=
| 1 |
| 2 |
故答案为:MN=
| 1 |
| 2 |
点评:考查了两点间的距离.首先要根据题意,考虑所有可能情况,画出正确图形.再根据中点的概念,进行线段的计算与证明.

练习册系列答案
相关题目
 如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y= 如图,点C、F在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠ACE=∠DFE.
如图,点C、F在BE上,BF=CE,AB=DE,∠B=∠E.求证:∠ACE=∠DFE. △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示. 平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=-
平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=- 我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.
我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.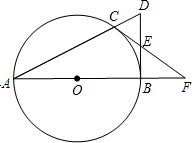 如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证:
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证: