题目内容
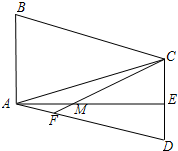 已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F.
已知:在?ABCD中,AE⊥CD,垂足为E,点M为AE上一点,且ME=AB,AM=CE,连接CM并延长交AD于点F.(1)若点E是CD的中点,求证:△ABC是等腰三角形.
(2)求证:∠AFM=3∠BCF.
考点:平行四边形的性质,全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:(1)易证△ADC是等腰三角形,所以AC=AD,根据平行四边形的性质可知:AD=BC,所以AC=BC,即△ABC是等腰三角形.
(2)连接BM,由已知条件可证明:△ABM≌△ECM,所以∠CME=∠AMF,再根据三角形外角之间的关系即可证明:∠AFM=3∠BCF.
(2)连接BM,由已知条件可证明:△ABM≌△ECM,所以∠CME=∠AMF,再根据三角形外角之间的关系即可证明:∠AFM=3∠BCF.
解答:证明: (1)∵AE⊥CD,CE=DE,
(1)∵AE⊥CD,CE=DE,
∴AC=AD,
∵四边形ABCD是平行四边形,
∴BC=AD,
∴AC=BC,
∴△ABC是等腰三角形;
(2)连接BM,
∵AB∥CD,
∴∠BAM=∠CEM,
在△ABM和△ECM中,
,
∴△ABM≌△ECM(SAS),
∵∠AMF=∠ACM+∠CAM,∠CME=∠AMF,
∴∠CME=∠ACM+∠CAM,
∵∠CAE=∠DAE,
∴∠AFM=3∠BCF.
 (1)∵AE⊥CD,CE=DE,
(1)∵AE⊥CD,CE=DE,∴AC=AD,
∵四边形ABCD是平行四边形,
∴BC=AD,
∴AC=BC,
∴△ABC是等腰三角形;
(2)连接BM,
∵AB∥CD,
∴∠BAM=∠CEM,
在△ABM和△ECM中,
|
∴△ABM≌△ECM(SAS),
∵∠AMF=∠ACM+∠CAM,∠CME=∠AMF,
∴∠CME=∠ACM+∠CAM,
∵∠CAE=∠DAE,
∴∠AFM=3∠BCF.
点评:本题考查了平行四边形的性质、等腰三角形的判定和性质、全等三角形的判定和性质,解题的关键是添加辅助线构造全等三角形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
下列运算中,正确的是( )
| A、a2+a2=2a4 |
| B、(ab2)2=a2b4 |
| C、a3÷a3=a |
| D、a2•a3=a6 |

 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示. 我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.
我市岑水高速公路建设中需要建造一座抛物线形拱桥涵洞,拱桥路面宽度为8米,现以AB所在直线x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,坐标原点为O,已知AB=8米,设抛物线的函数解析式为y=ax2+4.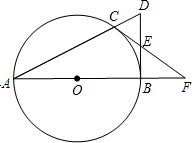 如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证:
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证: