题目内容
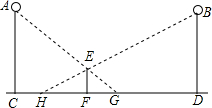如图，晚上，身高1.5米的小颖站在两盏相距25米的同样高的路灯之间．现测得她在路灯A照射下的影长FG为2米，她在路灯B照射下的影长FH为3米，则这两盏路灯的高度是考点：相似三角形的应用
专题：
分析：根据相似三角形的判定与性质得出
=
，
=
，进而求出HC的长，进而得出AC的长．
| EF |
| AC |
| FG |
| GC |
| EF |
| BD |
| FH |
| DB |
解答：解：∵EF∥AC，EF∥BD，
∴△EFG∽△ACG，△EFH∽△BDH，
∴
=
，
=
，
∴
=
，
∴
=
，
解得：HC=7，
∴
=
，
解得：AC=9，
故答案为：9．
∴△EFG∽△ACG，△EFH∽△BDH，
∴
| EF |
| AC |
| FG |
| GC |
| EF |
| BD |
| FH |
| DB |
∴
| FG |
| GC |
| FH |
| DB |
∴
| 2 |
| 5+CH |
| 3 |
| 25-HC |
解得：HC=7，
∴
| 1.5 |
| AC |
| 2 |
| 7+5 |
解得：AC=9，
故答案为：9．
点评：此题主要考查了相似三角形的应用，正确利用相似三角形的判定与性质得出CH的长是解题关键．
练习册系列答案
相关题目
平面上有任意四点，经过其中两点画一条直线，共可画（ ）
| A、1条直线 |
| B、6条直线 |
| C、6条或4条直线 |
| D、1条或4条或6条直线 |
如图，为了测量某建筑物CD的高度，在平地上A处测得建筑物顶端C的仰角为30°，沿AD方向前进12米到达B处，在B处测得建筑物顶端C的仰角为60°，则建筑物CD的高度为（ ）A、6
| ||
B、6
| ||
C、3
| ||
D、4
|
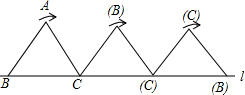如图，将边长为1cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为
如图，在平面直角坐标系xOy中，A（-1，5），B（-2，0），C（-4，3）．
如图，已知直线y=
如图，将边长为2的正方形ABCD的各边四等分，把一长度为| 34 |
| A、CR3 |
| B、R1D |
| C、R2R3 |
| D、R2R1 |
已知点P（2，2a-3）在第一象限，则a的取值范围是（ ）
| A、a＜-1 | ||
B、-1＜a＜
| ||
C、-
| ||
D、a＞
|