题目内容
 如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).
如图,在平面直角坐标系xOy中,A(-1,5),B(-2,0),C(-4,3).(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法).
(2)写出C′点的坐标:C′(
(3)△ABC的面积=
(4)在y轴上标出点P的位置,使PA+PB最小.
考点:作图-轴对称变换,轴对称-最短路线问题
专题:
分析:(1)利用关于y轴对称点的性质得出对应点,进而得出答案;
(2)利用所画图形,进而得出C′点坐标;
(3)利用矩形面积-周围三角形面积进而得出答案;
(4)利用轴对称求最短路径求出P点即可.
(2)利用所画图形,进而得出C′点坐标;
(3)利用矩形面积-周围三角形面积进而得出答案;
(4)利用轴对称求最短路径求出P点即可.
解答: 解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;
(2)C′(4,3);
(3)S△ABC=3×5-
(1×5+2×3+3×2)=
;
(4)如图所示:P点即为所求.
故答案为:
.
 解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;(2)C′(4,3);
(3)S△ABC=3×5-
| 1 |
| 2 |
| 13 |
| 2 |
(4)如图所示:P点即为所求.
故答案为:
| 13 |
| 2 |
点评:此题主要考查了轴对称变换以及三角形面积和轴对称求最短路径问题,得出对应点为位置是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
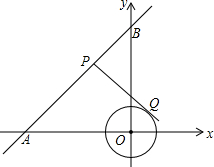 如图,在平面直角坐标系xOy中,直线AB过点A(-3
如图,在平面直角坐标系xOy中,直线AB过点A(-3| 2 |
| 2 |
A、
| ||
B、2
| ||
| C、3 | ||
D、
|
不解方程,一元二次方程3x2+2x+1=0的解的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
 如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1),把△A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到△ABC,试写出△A1B1C1三个顶点.
如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1),把△A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到△ABC,试写出△A1B1C1三个顶点.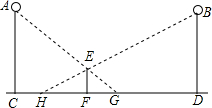 如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是
如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是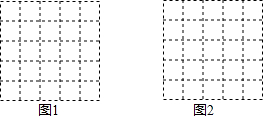 所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形.
所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形.