题目内容
 如图,为了测量某建筑物CD的高度,在平地上A处测得建筑物顶端C的仰角为30°,沿AD方向前进12米到达B处,在B处测得建筑物顶端C的仰角为60°,则建筑物CD的高度为( )
如图,为了测量某建筑物CD的高度,在平地上A处测得建筑物顶端C的仰角为30°,沿AD方向前进12米到达B处,在B处测得建筑物顶端C的仰角为60°,则建筑物CD的高度为( )A、6
| ||
B、6
| ||
C、3
| ||
D、4
|
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形:得出AB=BC=12m,进而得出sin60°=
,可求出CD的长,即可得出答案.
| CD |
| BC |
解答:解:根据题意可得:AB=12米,
∵∠CBD=∠A+∠ACB=60°,∠A=30°,
∴∠ACB=∠A=30°,
∴AB=BC=12米,
在Rt△CBD中,sin60°=
,
则CD=BC•sin60°=12×
=6
(米).
故选:A.
∵∠CBD=∠A+∠ACB=60°,∠A=30°,
∴∠ACB=∠A=30°,
∴AB=BC=12米,
在Rt△CBD中,sin60°=
| CD |
| BC |
则CD=BC•sin60°=12×
| ||
| 2 |
| 3 |
故选:A.
点评:本题考查了解直角三角形的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形,难度一般.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列四组线段中,可以构成直角三角形的是( )
| A、3,5,6 | ||
| B、2,3,4 | ||
C、1,
| ||
D、3,4,
|
若函数y=
的图象为C,则直线y=a(a为常数)与C的交点的个数为( )
|
| A、0或2个 |
| B、0或1或2个 |
| C、0或2或4个 |
| D、0或2或3或4个 |
 如图,这个几何体从上面看到的平面图形是( )
如图,这个几何体从上面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1),把△A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到△ABC,试写出△A1B1C1三个顶点.
如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1),把△A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到△ABC,试写出△A1B1C1三个顶点.
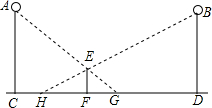 如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是
如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是