题目内容
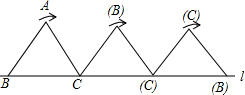 如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为
如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为考点:弧长的计算,等边三角形的性质,旋转的性质
专题:计算题
分析:点B从开始到结束,所经过路径为两段弧,第一段是以C点为圆心,1cm为半径,圆心角为120°的弧,第二段是以(A)点为圆心,1cm为半径,圆心角为120°的弧,然后根据弧长公式计算.
解答:解:∵△ABC为等边三角形,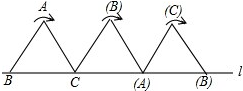
∴∠BCA=60°,
∴△ABC每次旋转的度数为120°,
点B从开始到结束,所经过路径的长度=
+
=
π(cm).
故答案为
πcm.

∴∠BCA=60°,
∴△ABC每次旋转的度数为120°,
点B从开始到结束,所经过路径的长度=
| 120•π•1 |
| 180 |
| 120•π•1 |
| 180 |
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:本题考查了弧长公式:l=
(弧长为l,圆心角度数为n,圆的半径为R).也考查了旋转的性质.
| nπR |
| 180 |

练习册系列答案
相关题目
 如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )| A、x<1 | B、x>1 |
| C、x≤1 | D、x≥1 |
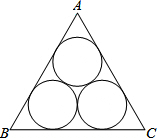 如图,三个半径为
如图,三个半径为| 3 |
A、12+6
| ||
B、12+12
| ||
C、18+12
| ||
D、18+6
|
 如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.
如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.
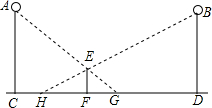 如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是
如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是 如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )
如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )