题目内容
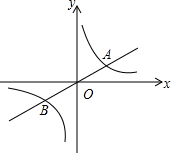 如图,已知直线y=
如图,已知直线y=| 1 |
| 2 |
| k |
| x |
(1)求k的值;
(2)若双曲线y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义可知S△COE=S△BOF,所以S梯形CEFB=S△BOC=15.
(2)根据k的几何意义可知S△COE=S△BOF,所以S梯形CEFB=S△BOC=15.
解答:解:(1)∵点A横坐标为4,
∴由y=
x可知当x=4时,y=2.
∴点A的坐标为(4,2).
∵点A是直线y=
x与双曲线y=
(k>0)的交点,
∴k=4×2=8.
(2)如图,
过点C、B分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y=
上,当y=-8时,x=-1.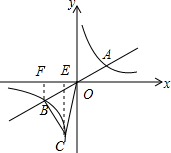
∴点C的坐标为(-1,-8).
∵点A的坐标为(4,2).
∴B(-4,-2),
∵点C、B都在双曲线y=
上,
∴S△COE=S△BOF=4.
∴S△COE+S梯形CEFB=S△COB+S△BOF.
∴S△COB=S梯形CEFB.
∵S梯形CEFB=
×(2+8)×3=15,
∴S△BOC=15.
∴由y=
| 1 |
| 2 |
∴点A的坐标为(4,2).
∵点A是直线y=
| 1 |
| 2 |
| k |
| x |
∴k=4×2=8.
(2)如图,
过点C、B分别作x轴的垂线,垂足为E、F,
∵点C在双曲线y=
| 8 |
| x |

∴点C的坐标为(-1,-8).
∵点A的坐标为(4,2).
∴B(-4,-2),
∵点C、B都在双曲线y=
| 8 |
| x |
∴S△COE=S△BOF=4.
∴S△COE+S梯形CEFB=S△COB+S△BOF.
∴S△COB=S梯形CEFB.
∵S梯形CEFB=
| 1 |
| 2 |
∴S△BOC=15.
点评:主要考查了待定系数法求反比例函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
若函数y=
的图象为C,则直线y=a(a为常数)与C的交点的个数为( )
|
| A、0或2个 |
| B、0或1或2个 |
| C、0或2或4个 |
| D、0或2或3或4个 |
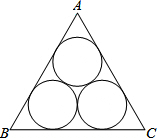 如图,三个半径为
如图,三个半径为| 3 |
A、12+6
| ||
B、12+12
| ||
C、18+12
| ||
D、18+6
|
 如图,这个几何体从上面看到的平面图形是( )
如图,这个几何体从上面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是( )| A、8 | B、9 | C、10 | D、8 |

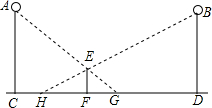 如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是
如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是 所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形.
所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形. 如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )
如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )