题目内容
18. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
分析 首先根据等式的性质可得∠BAD=∠CAE,然后再利用SAS定理判定△BAD≌△CAE,进而可得∠AEC=∠ADB=90°,在EF上截取CN=CF,由△BAD≌△CAE可得BD=CE,∠ADB=∠AEC=90°,再证明△BDF≌△CEN,推出BF=CN=CF即可.
解答  证明:∵∠BAC=∠DAE,
证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴∠AEC=∠ADB,
∵BD⊥AD,
∴∠ADB=90°,
∴∠AEC=90°,
在EF上截取CN=CF,
∵△BAD≌△CAE,
∴BD=CE,∠ADB=∠AEC=90°,
∴∠AED+∠DEC=90°,∠BDF+∠ADE=180°-∠BDA=90°,
∵AD=AE,
∴∠ADE=∠AED,
∴∠BDF=∠NEC,
在△BDF和△CEN中,$\left\{\begin{array}{l}{∠BFD=∠CNE}\\{∠BDF=∠CEN}\\{BD=CE}\\{\;}\end{array}\right.$,
∴△BDF≌△CEN(AAS),
∴BF=CN=CF,
即BF=CF.
点评 此题主要考查了全等三角形的判定与性质,关键是正确掌握全等三角形的判定定理,作出辅助线.

练习册系列答案
相关题目
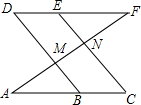 如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC.
如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC.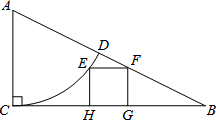 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4. 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF. 如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形.
如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形. 如图,已知∠ABD=∠ACE,且AD=AE,求证:PB=PC.
如图,已知∠ABD=∠ACE,且AD=AE,求证:PB=PC. 已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP.
已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP. 已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.