题目内容
7. 已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
已知△ABC中,∠ABC=45°,AB=$\frac{5}{2}$$\sqrt{2}$,BC=12,将线段AC绕点A逆时针旋转90°,线段AD,连接BD,求BD的长.
分析 如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN的延长线于E,易证明△ADN≌△CAM,四边形MNEB是矩形,在RT△EBD中求出BE,ED即可.
解答 解:如图作AM⊥BC垂足为M,DN⊥MA交MA的延长线于N,BE⊥DN交DN的延长线于E.
∵∠E=∠ENM=∠NMB=90°,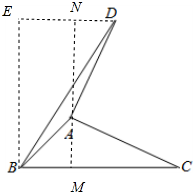
∴四边形MNEB是矩形,
BM=EN,EB=MN,
∵∠DAC=90°,
∴∠DAN+∠MAC=90°,
∵∠MAC+∠ACM=90°,
∴∠DAN=∠ACM,
在△ADN和△CAM中,
$\left\{\begin{array}{l}{∠DNA=∠AMC}\\{∠DAN=∠ACM}\\{AD=AC}\end{array}\right.$,
∴△ADN≌△CAM,
AM=DN,AN=CM.
在RT△ABM中,∵AB=$\frac{5\sqrt{2}}{2}$,∠ABM=45°,
∴BM=AM=$\frac{5}{2}$,MC=BC-BM=$\frac{19}{2}$,
在RT△BDE中,∵EB=MN=12,ED=5
∴BD=$\sqrt{B{E}^{2}+E{D}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13.
点评 本题考查全等三角形的判定和性质、矩形的判定和性质、勾股定理等知识,添加辅助线构造全等三角形是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
17.以$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$为解的二元一次方程组是( )
| A. | $\left\{\begin{array}{l}x+y=5\\ x-y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=5\\ x-y=-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=-5\\ x-y=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=-5\\ x-y=-1\end{array}\right.$ |
 如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.
如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.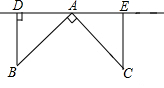 如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.
如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE. 如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证:
如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证: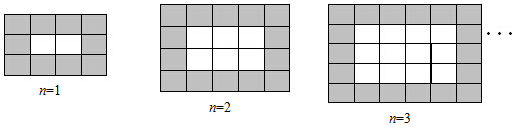
 把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分染成红色,那么红色部分的面积为33.
把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分染成红色,那么红色部分的面积为33.