题目内容
13. 如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形.
如图,△ABC与△BDE为等边三角形,连接AD,EC,AD中点为M,EC中点为N,BM,BN,MN,求证:△BMN为等边三角形.
分析 由等边三角形的性质得出AB=BC,∠ABC=∠DBE=60°,BD=BE,得出∠ABD=∠CBE,由SAS证明△ABD≌△CBE,得出AD=CE,∠BAM=∠BCN,由已知条件得出AM=CN,由SAS证明△ABM≌△CBN,得出BM=BN(即△BMN是等边三角形),∠ABM=∠CBN,证出∠MBN=60°,即可得出结论.
解答 证明:∵△ABC与△BDE为等边三角形,
∴AB=BC,∠ABC=∠DBE=60°,BD=BE,
∴∠ABD=∠CBE,
在△ABD和△CBE中,$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABD=∠CBE}&{\;}\\{BD=BE}&{\;}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴AD=CE,∠BAM=∠BCN,
∵AD中点为M,EC中点为N,
∴AM=$\frac{1}{2}$AD,CN=$\frac{1}{2}$CE,
∴AM=CN,
在△ABM和△CBN中,$\left\{\begin{array}{l}{AM=CN}&{\;}\\{∠BAM=∠BCN}&{\;}\\{AB=CB}&{\;}\end{array}\right.$,
∴△ABM≌△CBN(SAS),
∴BM=BN(即△BMN是等边三角形),∠ABM=∠CBN,
∵∠ABM+∠ABN=∠CBN+∠ABN=∠ABC=60°,
即∠MBN=60°,
∴△BMN为等边三角形.
点评 本题考查了全等三角形的判定与性质、等边三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
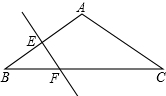 如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长.
如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长. 如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.
如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点. 如图,AB=DC,AC=DB,由此你能猜想出什么结论?并简要说明理由.
如图,AB=DC,AC=DB,由此你能猜想出什么结论?并简要说明理由.
 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由. 已知:如图,∠1=∠3,∠E=∠C,AD=AB,求证:BC=DE.
已知:如图,∠1=∠3,∠E=∠C,AD=AB,求证:BC=DE. 如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证:
如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AE、CF相交于点O.求证: 如图,四边形ABCD中,AD=CD,∠ADB=∠ACB,AC∥DE.求证:AD2=AF•DE.
如图,四边形ABCD中,AD=CD,∠ADB=∠ACB,AC∥DE.求证:AD2=AF•DE.