题目内容
7.一个多边形的内角和与外角和的和为720度,求这个多边形的边数.分析 首先设这个多边形的边数有n条,根据多边形内角和公式(n-2)•180°可得内角和,再根据外角和为360°可得方程(n-2)•180+360=720,再解方程即可.
解答 解:设这个多边形的边数有n条,由题意得:
(n-2)•180+360=720,
解得:n=4,
点评 此题主要考查了多边形的内角和和外角和,关键是掌握多边形的内角和公式与外角和定理.

练习册系列答案
相关题目
17.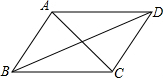 如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
 如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )
如图,已知?ABCD,在分别以四个顶点为起点和终点的向量中,向量$\overrightarrow{BD}$=( )| A. | $\overrightarrow{BA}$+$\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CB}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$ |
 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E. 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.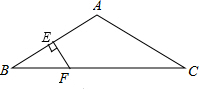 如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.
如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF. 如图,在?ABCD中,AD=10,AC=8,BD=14,则△BOC的周长是21.
如图,在?ABCD中,AD=10,AC=8,BD=14,则△BOC的周长是21.