题目内容
2.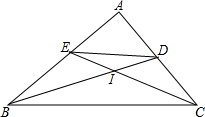 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
分析 在BC上截取BM=BE、CN=CD,根据SAS定理可以证明△BIE≌△BIM,△CID≌△CIN,再根据全等三角形对应边相等得到EI=MI,DI=NI,全等三角形对应角相等,推出∠EID与∠MIN互补,从而得到△DIE与△MIN的面积相等,最后求出四边形BCDE的面积等于△BIC的面积的2倍.
解答 解:如图,在BC上截取BM=BE、CN=CD,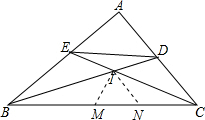
∵BD,CE分别为两内角平分线,
则△BIE≌△BIM(SAS),△CID≌△CIN(SAS),
∵∠BIM=∠BIE=45°,∠CIN=∠CID=45°,
即∠EIM=∠DIN=90°,
∴∠DIE+∠MIN=180°,
∴S△DIE=S△MIN,
∴S四边形BCDE=2S△BCI=2S.
点评 本题主要考查了三角形内心的性质和全等三角形的判定与性质,读懂题目信息是解题的关键,根据信息作辅助线构造出符合信息的图形是本题的难点.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
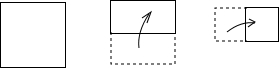
14.将正方形纸片如图所示由下往上对折,再由左向右对折,称为完成一次操作,按上述规则完成三次操作以后,剪去所得小正方形的左下角,问:当展开这张正方形纸片后,小洞孔一共有( )

| A. | 3个 | B. | 4个 | C. | 16个 | D. | 64个 |
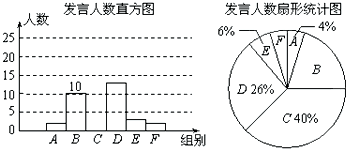
11.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言的人数比为10:3,请结合图中相关数据回答下列问题:
(1)A组有2人,C组有20人,E组有3人,并补全直方图;
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.
| 课堂发言次数n | |
| A | 0≤n<5 |
| B | 5≤n<10 |
| C | 10≤n<15 |
| D | 15≤n<20 |
| E | 20≤n<25 |
| F | 25≤n<30 |
(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;
(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.

 如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$.
如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$. 如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足分别为D、E,求证:△AFE∽△CBD.
如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足分别为D、E,求证:△AFE∽△CBD.
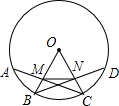 如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.
如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.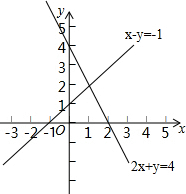 直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.