题目内容
14. 如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$.
如图是单位长度为1的网格,在图中画一个格点三角形ABC,使其周长等于7+$\sqrt{13}$.
分析 利用网格结构与勾股定理画出△ABC,使得AB=2,AC=$\sqrt{13}$,BC=5即可.
解答 解:如图所示,AB=2,AC=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以△ABC的周长=2+$\sqrt{13}$+5=7+$\sqrt{13}$.
则△ABC为所求三角形.
点评 此题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
5.二次函数y=ax2+bx+c图象上部分点的对应值如下表
则使y<0的x的取值范围为( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| A. | x<0 | B. | x>$\frac{1}{2}$ | C. | -2<x<3 | D. | x<-2或x>3 |
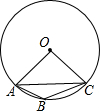 如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由.
如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由. 如图,方格纸中每个小方格的边长为1,画一条长为$\sqrt{18}$的线段.
如图,方格纸中每个小方格的边长为1,画一条长为$\sqrt{18}$的线段.
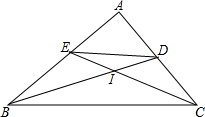 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.