题目内容
12. 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.(1)求BD的长;
(2)求S△BOD的值.
分析 (1)根据中线的概念求出AB、AC的长,根据周长公式求出BC,根据重心的概念得到AD是BC边上的中线,得到答案;
(2)根据三角形的中线把三角形分为面积相等的两部分和重心的性质计算即可.
解答 解:(1)BE、CF分别为AC、AB边的中线,
∴AB=2AF=6cm,AC=2AE=4cm,又△ABC的周长为18cm,
∴BC=8cm,
∵中线BE、CF相交于点O,
∴点O是三角形的重心,
∴AD是BC边上的中线,
∴BD=$\frac{1}{2}$CB=4cm;
(2)∵AD是BC边上的中线,S△ABC=36cm2,
∴S△ABD=18cm2.
∵点O是三角形的重心,
∴AO=2OD,
∴S△BOD=6cm2.
点评 本题考查的是三角形的重心和三角形的面积的计算,掌握三角形的重心是三角形三条中线的交点、三角形的中线把三角形分为面积相等的两部分是解题的关键.

练习册系列答案
相关题目
1.设a<b,下列不等式变形错误的是( )
| A. | a-12<b-12 | B. | a+7<b+7 | C. | -12a<-12b | D. | 7a<7b |
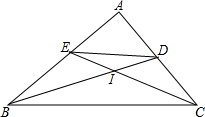 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.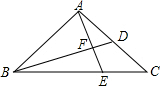 如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.
如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$. 如图,△ABC≌△DEF,AB=4,BC=3.
如图,△ABC≌△DEF,AB=4,BC=3.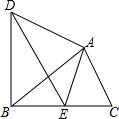 如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.
如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.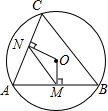 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12.
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC垂足分别为M、N,如果MN=6,那么BC=12.