题目内容
7.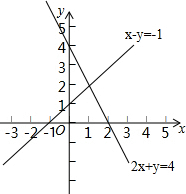 直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
分析 先利用函数图象得到交点坐标,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案.
解答 解:如图,直线x-y=-1与直线2x+y=4的交点P的坐标为(1,2),所以二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.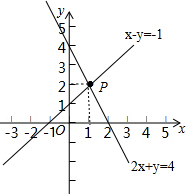
故答案为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
17.对式子“-7+10-8-2”的读法正确的是( )
| A. | 负7加10减8减2 | B. | 负7正10负8减2 | ||
| C. | 负7,加10,负8,负2的和 | D. | 减7加10减8减2 |
12. 如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
 如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )| A. | 7.5 | B. | 8 | C. | 10 | D. | 15 |
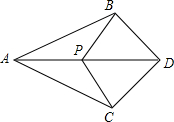 如图,AB=AC,AD平分∠BAC,P是AD上的一点,求证:∠PBD=∠PCD.
如图,AB=AC,AD平分∠BAC,P是AD上的一点,求证:∠PBD=∠PCD.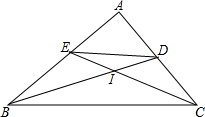 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积. 如图,在平行四边形ABCD中,BD是对角线,E、F是BD上的两点,DE=BF.求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,BD是对角线,E、F是BD上的两点,DE=BF.求证:四边形AFCE是平行四边形.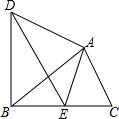 如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.
如图,△ABC绕点A顺时针旋转得△ADE,点E恰好落在边BC上.