题目内容
12.如图:AD是△ABC中BC边上的中线,A′D′是△A′B′C′中B′C′边上的中线,$\frac{AB}{A′B′}=\frac{AC}{A′C′}=\frac{AD}{A′D′}$,试说明△ABC∽△A′B′C′.
分析 延长AD到E使DE=AD,连结BE,延长A′D′到E′,使D′E′=A′D′,如图,先证明△BDE≌△CDA得到BE=AC,∠EBD=∠C,同理可得B′E′=A′C′,∠E′B′D′=∠C′,于是利用$\frac{AB}{A′B′}=\frac{AC}{A′C′}=\frac{AD}{A′D′}$可得$\frac{AB}{A′B′}$=$\frac{BE}{B′E′}$=$\frac{AE}{A′E′}$,则根据三组对应边的比相等的两个三角形相似得到△ABE∽△A′B′E′,得到∠ABE=∠A′B′E′,接着根据三角形内角和定理得∠BAC=∠B′A′C′,然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABC∽△A′B′C′.
解答 证明: 延长AD到E使DE=AD,连结BE,延长A′D′到E′,使D′E′=A′D′,如图,
延长AD到E使DE=AD,连结BE,延长A′D′到E′,使D′E′=A′D′,如图,
∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△BDE和△CDA中
$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDA}\\{DE=DA}\end{array}\right.$,
∴△BDE≌△CDA,
∴BE=AC,∠EBD=∠C,
同理可得△B′D′E′≌△C′D′A′,
∴B′E′=A′C′,∠E′B′D′=∠C′,
∵$\frac{AB}{A′B′}=\frac{AC}{A′C′}=\frac{AD}{A′D′}$,
∴$\frac{AB}{A′B′}$=$\frac{BE}{B′E′}$=$\frac{AE}{A′E′}$,
∴△ABE∽△A′B′E′,
∴∠ABE=∠A′B′E′,
∴∠ABC+∠C=∠A′B′C′+∠C′,
∴∠BAC=∠B′A′C′,
而$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了全等三角形的判定与性质.

 名校课堂系列答案
名校课堂系列答案| A. | 负7加10减8减2 | B. | 负7正10负8减2 | ||
| C. | 负7,加10,负8,负2的和 | D. | 减7加10减8减2 |
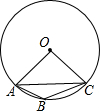 如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由.
如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由.
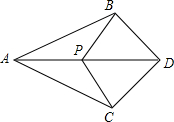 如图,AB=AC,AD平分∠BAC,P是AD上的一点,求证:∠PBD=∠PCD.
如图,AB=AC,AD平分∠BAC,P是AD上的一点,求证:∠PBD=∠PCD.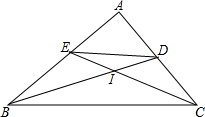 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积. 如图,在平行四边形ABCD中,BD是对角线,E、F是BD上的两点,DE=BF.求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,BD是对角线,E、F是BD上的两点,DE=BF.求证:四边形AFCE是平行四边形.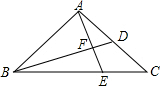 如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.
如图,在△ABC中,BD为AC边上的中线,BE=AB,且AE与BD相交于点F,求证:$\frac{AB}{BC}$=$\frac{EF}{AF}$.