题目内容
因式分解:(x2+x+1)(x2+x+2)-12.
考点:因式分解-十字相乘法等
专题:
分析:首先将x2+x看作整体,进而去括号,利用十字相乘法分解因式得出即可.
解答:解:(x2+x+1)(x2+x+2)-12
=(x2+x)2+3(x2+x)-10
=(x2+x-2)(x2+x+5)
=(x-1)(x+2)(x2+x+5).
=(x2+x)2+3(x2+x)-10
=(x2+x-2)(x2+x+5)
=(x-1)(x+2)(x2+x+5).
点评:此题主要考查了十字相乘法分解因式,正确应用十字相乘法是解题关键.

练习册系列答案
相关题目
 如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB=
如图,线段AC、BD为四边形ABCD对角线.已知,∠ABC=∠ADC=90°,AD=DC,tan∠ACB= 一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少?
一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少?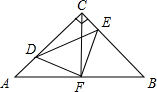 如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,F是AB边的中点,D、E分别在边AC、BC上运动,且始终保持AD=CE,连接CF,DF,EF和DE
如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,F是AB边的中点,D、E分别在边AC、BC上运动,且始终保持AD=CE,连接CF,DF,EF和DE