题目内容
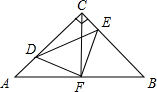 如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,F是AB边的中点,D、E分别在边AC、BC上运动,且始终保持AD=CE,连接CF,DF,EF和DE
如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,F是AB边的中点,D、E分别在边AC、BC上运动,且始终保持AD=CE,连接CF,DF,EF和DE(1)求证:△ADF≌△CEF;
(2)判断△DEF的形状并说明理由.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据F是AB中点,可得AF=BF=CF,∠A=∠FCE=45°,即可证明△ADF≌△CEF;
(2)根据△ADF≌△CEF可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可解题.
(2)根据△ADF≌△CEF可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可解题.
解答:证明:(1)∵F是AB中点,AC=BC,∠ACB=90°,
∴AF=BF=CF,∠A=∠FCE=45°,
在△ADF和△CEF中,
,
∴△ADF≌△CEF(SAS);
(2)∵△ADF≌△CEF,
∴DF=EF,∠AFD=∠CFE,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFE=90°,即∠DFE=90°,
∴△DEF是等腰直角三角形.
∴AF=BF=CF,∠A=∠FCE=45°,
在△ADF和△CEF中,
|
∴△ADF≌△CEF(SAS);
(2)∵△ADF≌△CEF,
∴DF=EF,∠AFD=∠CFE,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFE=90°,即∠DFE=90°,
∴△DEF是等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADF≌△CEF是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图可以拼成的几何体是( )
如图可以拼成的几何体是( )| A、三梭柱 | B、四棱柱 |
| C、圆柱 | D、圆锥 |
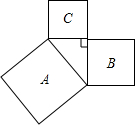 如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )
如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )| A、12 | B、13 | C、144 | D、19 |
 如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )
如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )| A、88° | B、71° |
| C、44° | D、72° |
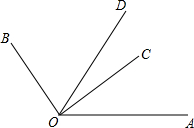 如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数.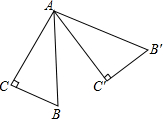 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转70°后得到△AB′C′,则∠CAB′=
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转70°后得到△AB′C′,则∠CAB′=