题目内容
 一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少?
一张长方形纸长26厘米,宽19厘米,将这张纸四角沿图中虚线对折,那么四条虚线所围成的正方形的面积是多少?考点:翻折变换(折叠问题)
专题:
分析:设长方形为ABCD,小三角形的底边在AB上为EF,阴影部分为MNQP.因为四角沿图中的虚线对折,所以AF=AD,BE=BC,∠DAF=∠EBC=90°,又因为AB=CD=26,AD=BC=19,所以AF=AD=BE=BC=19,所以EF=(2×19-26)÷2=6,所以MNQP是正方形,从而计算出正方形MNQP的面积.
解答: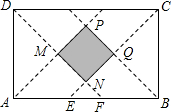 解:设长方形为ABCD,小三角形的底边在AB上为EF,阴影正方形为MNQP.
解:设长方形为ABCD,小三角形的底边在AB上为EF,阴影正方形为MNQP.
∵四角沿图中的虚线对折,
∴AF=AD,BE=BC,∠DAF=∠EBC=90°,
又∵AB=CD=26,AD=BC=19,
∴AF=AD=BE=BC=19,
∴EF=(2×19-26)÷2=6,
∴MNQP是正方形,
∴NE=NF=MF-MN,且∠ENF=90°,
∴△ADF和△ENF是等腰直角三角形,
∴EN=FN=
=
=3
,
∴DF=BE=
=
=19
,
∴MN=MF-NF=DF÷2-NF=19
÷2-3
=6.5
,
∴S正方形MNQP=24.5 cm2.
答:四条虚线所围成阴影正方形的面积是24.5cm2.
 解:设长方形为ABCD,小三角形的底边在AB上为EF,阴影正方形为MNQP.
解:设长方形为ABCD,小三角形的底边在AB上为EF,阴影正方形为MNQP.∵四角沿图中的虚线对折,
∴AF=AD,BE=BC,∠DAF=∠EBC=90°,
又∵AB=CD=26,AD=BC=19,
∴AF=AD=BE=BC=19,
∴EF=(2×19-26)÷2=6,
∴MNQP是正方形,
∴NE=NF=MF-MN,且∠ENF=90°,
∴△ADF和△ENF是等腰直角三角形,
∴EN=FN=
|
|
| 2 |
∴DF=BE=
| 2AD2 |
| 2×192 |
| 2 |
∴MN=MF-NF=DF÷2-NF=19
| 2 |
| 2 |
| 2 |
∴S正方形MNQP=24.5 cm2.
答:四条虚线所围成阴影正方形的面积是24.5cm2.
点评:本题考查的是翻折变换,解答此题的关键是根据图形对折后求出NE=NF=MF-MN,且∠ENF=90°得到△ENF是等腰直角三角形,然后求出MN的长度,进而求出阴影部分的面积.

练习册系列答案
相关题目
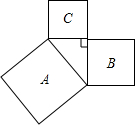 如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )
如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )| A、12 | B、13 | C、144 | D、19 |
 如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.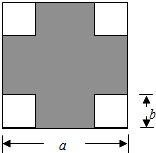 如图,在一块边长为a的正方形纸板四角,各剪去一个边长为b(b<
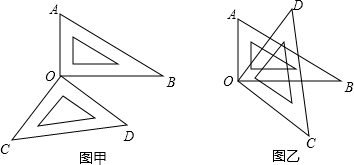
如图,在一块边长为a的正方形纸板四角,各剪去一个边长为b(b<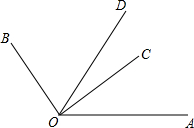 如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数.
如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°20′,求∠AOB的度数.