题目内容
15.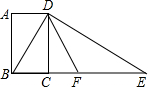 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.
分析 根据矩形的性质得到CD=AB=x,BC=AD=y,然后利用直角△BDE的斜边上的中线等于斜边的一半得到BF=DF=EF=3,则在直角△DCF中,利用勾股定理求得x2+(y-3)2的值.
解答 解:∵四边形ABCD是矩形,AB=x,AD=y,
∴CD=AB=x,BC=AD=y,∠BCD=90°.
又∵BD⊥DE,点F是BE的中点,DF=3,
∴BF=DF=EF=3.
∴CF=4-BC=3-y.
∴在直角△DCF中,DC2+CF2=DF2,即x2+(3-y)2=32=9,
∴x2+(y-3)2=x2+(3-y)2=9.
故答案是:9.
点评 本题考查了勾股定理,直角三角形斜边上的中线以及矩形的性质,根据“直角△BDE的斜边上的中线等于斜边的一半”求得BF的长是解题的关键.

练习册系列答案
相关题目
10.菱形的对角线AC=8cm,BD=6cm,AC、BD相交于点O,则点O到任一边中点的距离为( )
| A. | 2.5cm | B. | 2.4cm | C. | 5cm | D. | 3cm |
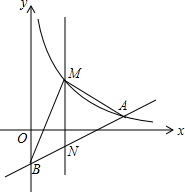 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.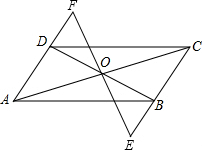 如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?
如图,在?ABCD中,对角线AC,BD交于点O,过点O的直线分别交CB,AD的延长线于点E,F,BE与DF相等吗?为什么?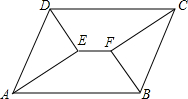 如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC.
如图,?ABCD中,AB>AD,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.请证明:EF=AB-BC. 已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求:
已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求: 如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.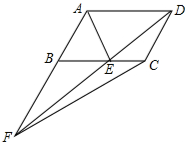 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.