题目内容
17.在平行四边形ABCD中,对角线AC,BD相交于点O,若BD与AC的和为18,CD:DA=2:3,△AOB的周长为13,则BC的长为6.分析 根据平行四边形的性质可得AB=CD,AD=BC,AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}BD$,然后再根据条件求出AO+BO的长,进而可得AB的长,从而得到CD的长,再根据CD:DA=2:3可得AD的长,进而可得BC的长.
解答 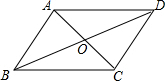 解:如图:
解:如图:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}BD$,
∵BD与AC的和为18,
∴AO+BO=$\frac{1}{2}×$18=9,
∵△AOB的周长为13,
∴AB=13-9=4,
∴CD=4,
∵CD:DA=2:3,
∴AD=6,
∴BC=6,
故答案为:6.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.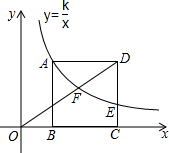 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )| A. | ($\frac{2\sqrt{3}}{3},\sqrt{3}$) | B. | ($\sqrt{3},\frac{2\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{3}}{3},2\sqrt{3}$) | D. | (2$\sqrt{3},\frac{\sqrt{3}}{3}$) |
7.已知不等式2x+a<3x的解为x>1,则a的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
 如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.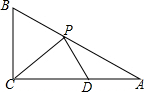 如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.
如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.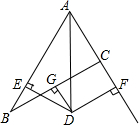 如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.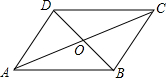 已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.