题目内容
15.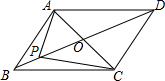 如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点
如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点(1)求证:S△AOB=S△BOC;
(2)设P为对角线BD上任意一点(点P与点B、D不重合),试猜想S△APB与S△BPC的大小关系,并说明理由.
分析 (1)由平行四边形的性质可知AO=CO,则等底同高的三角形面积相等,问题得证;
(2)S△APB=S△BPC,根据同底等高的三角形面积相等即可证明.
解答 (1)证明:
∵四边形ABCD是平行四边形,点O为对角线AC、BD的交点,
∴AO=CO,
设△ABC边AC上的高为h,
∵S△AOB=$\frac{1}{2}$AO•h,S△BOC=$\frac{1}{2}$CO•h,
∴S△AOB=S△BOC;
(2)S△APB=S△BPC,理由如下:
设△ABP边上的高为m,△BPC边上的高为n
∵四边形ABCD是平行四边形,
∴m=n,
∴S△APB=S△BPC(同底等高).
点评 本题考查了平行四边形的性质以及三角形面积公式的运用,熟记等底同高的三角形面积相等以及同底等高的三角形面积相等是解题关键.

练习册系列答案
相关题目
3.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )
| A. | 18 | B. | 15 | C. | 12 | D. | 9 |
7.已知不等式2x+a<3x的解为x>1,则a的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
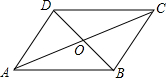 已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.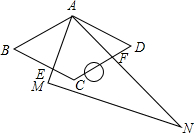 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.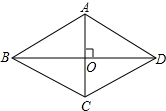 如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.